INTRODUCCIÓN
En la actualidad se requiere de una enseñanza que propicie en el estudiante un aprendizaje significativo. Se hace necesario enseñar la estadística con ejemplos o situaciones de la vida real. Este trabajo es una contribución al trabajo de Mvududu, y Kanyongo (2011), en respuesta a los esfuerzos encaminados a lograr una enseñanza de la estadística basada en los datos y en la comprensión de los conceptos, en un escenario contextualizado, y no en fórmulas sin sentido. La preocupación por la educación estadística no es reciente. Como bien señala Batanero (2001) .Existe el antecedente de esta preocupación desde la fundación en 1885, del Instituto Internacional de Estadística, ISI por sus siglas en inglés, la cual se materializa en 1948, con la creación del Comité de Educación, que se encargó de promover la formación estadística en los países en vías de desarrollo.
En la reforma de la educación estadística, se enfatiza el desarrollo del pensamiento estadístico y el conocimiento conceptual, en lugar de meros procedimientos. En otras palabras, sustentar la enseñanza - aprendizaje de la estadística en datos y en el razonamiento estadístico y no en la presentación de una cantidad abrumadora de métodos e incluso de teorías matemáticas, cuando se trate de cursos de nivel elemental o intermedio. Estas indicaciones y otras, tales como: fomentar el aprendizaje activo en el salón de clases, el uso de tecnologías para el desarrollo de la comprensión de conceptos y el análisis de datos, entre otras, aparecen en el Reporte de la Guía para la Evaluación e Instrucción en la Educación Estadística, GAISE por sus siglas en inglés (Garfield, Aliaga, Cobb, Cuff, Gould, Lock, Moore, Rossman,Stephenson, Utts, Velleman, and Witmer).
Lo que actualmente se pretende con la educación estadística es la preparación de un ciudadano que pueda dar respuesta a problemas que se presentan en la realidad; en este sentido, el estudiante tiene que desarrollar las competencias necesarias para entender y extraer el significado exacto de un argumento estadístico, comunicar resultados de un análisis estadístico y hacerlo en contexto, así como ser capaz de leer, interpretar y criticar documentos que incluyan información estadística, (Mvududu y Kayongo,2011).
Para el logro de estas competencias en el estudiante, se requiere una enseñanza en contexto, donde el estudiante aprenda estadística aplicándola en la solución de diversos problemas que suelen presentarse en la vida cotidiana (Gal y Ginsburg, 1994), de modo que construya su propio conocimiento mediante la resolución de problemas. Según Welsh (1996, p. 31), las componentes de un problema de inferencia son: una cuestión sustantiva, entendida como un problema al cual hay que dar solución; un conjunto de datos que respondan a la realización de una variable aleatoria con una distribución de probabilidad F y un modelo, es decir, una familia de distribuciones de probabilidad a la cual pertenece dicho modelo. Este planteamiento de Welsh, reafirma la propuesta de que si se quiere aprender estadística, hay que resolver problemas. Otro aspecto importante consiste en mantener el interés en el estudiante y por ende la motivación, hacia la resolución de los problemas que se le formulen (Symanzik y Vukasinovic, 2006); (Everson, Zieffler, and Garfield, 2008).
DESARROLLO
El problema: La estadística posibilita el estudio de la asociación entre variables mediante el método de la regresión y el uso de algunos de los estadísticos de correlación. Con la regresión se puede determinar la forma de dicha asociación y en consecuencia poder hacer predicciones. Con los estadísticos de correlación se puede medir la intensidad de la asociación. El estadístico de correlación muestral de Pearson, o coeficiente de correlación lineal, permite cuantificar la intensidad de la asociación lineal entre dos características expresadas al menos en una escala de intervalo. En cualquier curso de estadística se incluye el estudio de este coeficiente de correlación, el cual no siempre es bien entendido por los estudiantes. En el mejor de los casos el estudiante aprende a utilizar la fórmula de cálculo, incluso a interpretar el resultado de este cálculo aritmético, sin embargo, esta interpretación la realiza de forma mecánica, sin conocimiento de causa.
En la actualidad existen muchos paquetes computacionales, tanto comerciales como libres, que facilitan el trabajo en estadística, pero que adicionalmente, su uso en la enseñanza propicia la introducción de la tecnología como herramienta para el desarrollo de la comprensión de conceptos y el análisis de datos. No obstante, el uso indiscriminado de estos paquetes computacionales, sin conocimiento de los fundamentos de las diferentes técnicas y métodos estadísticos, puede conducir a malas interpretaciones de los resultados obtenidos, o aplicaciones erróneas de las diferentes técnicas, al violarse los supuestos que las sustentan. En este trabajo se ofrece un ejemplo en contexto para la enseñanza – aprendizaje del coeficiente de correlación lineal de Pearson. El nivel de enseñanza que se asume en el trabajo es el de un curso introductorio o elemental de estadística, para el logro de un aprendizaje significativo en el estudiante.
El coeficiente de correlación lineal: una síntesisEl coeficiente de correlación lineal es un estadístico que mide la intensidad de la asociación lineal entre dos características o variables, expresadas al menos en una escala de intervalo, a partir de la observación de cada una de ellas en las unidades que conforman una muestra aleatoria. Existen muchos libros de estadística que abordan este tema, (Guerra, Menéndez, Barrero y Egaña, 1998, pp. 226-239), (DeGroot, 1998, pp. 202 - 206), (Aaron, Aaron, and Coups, 2008, pp. 66 - 87), por sólo mencionar algunos. La expresión más generalizada para el cálculo del coeficiente de correlación lineal (r), involucra a la covarianza entre las características observadas X y Y, y la desviación estándar de cada una de ellas.
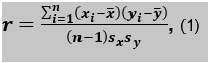, (1)
Donde ,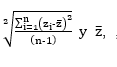
,para z= x, y, representan la desviación estándar y la media de X y Y respectivamente, y 
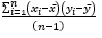a la covarianza entre ellas. El uso de esta fórmula en la enseñanza del coeficiente de correlación lineal es importante, porque en ella se puede destacar el concepto de covarianza, la cual indica la covariación de las variables involucradas; variables asociadas positivamente es indicado por la covarianza con un valor positivo y variables asociadas negativamente por un valor negativo. En el primer caso se trata de variables que al crecer una crece la otra y en el segundo caso, al crecer una decrece la otra. Si en (1) se denota la covarianza entre X y Y como s_xy
, se obtiene como expresión para r la siguiente:
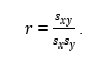
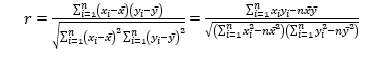(2) 
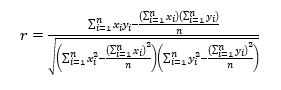(3)Valga recordar que el coeficiente de correlación lineal r satisface tres propiedades importantes. La primera de ella es que está acotado, esto es -1≤r≤1, la segunda se refiere a que no depende de la escala de medida para X y Yy la tercera que la medida de la relación sea independiente de la elección del origen para las variables X y Y.
El ejemplo En una investigación sobre el aprovechamiento docente de estudiantes, los investigadores que conducen dicho estudio, conjeturan que los estudiantes que obtienen altas calificaciones para las matemáticas, también las obtienen en física. Una muestra de ocho estudiantes arrojó las siguientes calificaciones.
Matemáticas |
6.7 |
20.0 |
26.7 |
40.0 |
53.3 |
60.0 |
73.3 |
93.3 |
Física |
6.7 |
13.3 |
26.7 |
26.7 |
33.3 |
46.7 |
53.3 |
60.0 |
De lo que se trata es, de dar una respuesta a estos investigadores sobre su conjetura, a la luz de la evidencia que puedan brindar los datos. A continuación se enuncian los pasos a seguir por el docente en la solución del problema desde una perspectiva estadística.
El docente debe inducir a los estudiantes a que, desde una perspectiva estadística, la respuesta a la inquietud de los investigadores puede brindarse mediante el empleo de un estadístico, el cual indique evidencia de si existe tal relación entre las calificaciones obtenidas por los estudiantes en matemáticas y física.
Destacar que si las variables, en este caso calificación en matemáticas y en física, tienen alguna relación lineal lo puedan hacer de forma directa o inversa, es decir, en el primer caso que al aumentar (disminuir) una de las variables la otra también aumente (disminuya); y en el segundo caso, cuando una de las dos aumente (disminuya) la otra disminuya (aumente). Es lógico pensar que si ambas variables tienen una relación directa o como también se dice positiva, el producto de sus valores sea positivo y como es de esperar la suma de todos estos productos sea positivo. En caso de que las variables tengan una relación inversa o negativa, el producto de sus valores será negativo y la suma de todos ellos también arrojará un valor negativo.
-
Destacar que siempre que se desee realizar un análisis estadístico, una exploración de la información suele resultar de mucha utilidad para descubrir patrones de comportamiento de los datos, cumplimientos de supuestos que requieran diferentes métodos estadísticos, etc. En el caso que nos ocupa, un gráfico de dispersión, esto es, un gráfico donde se muestren los puntos (x, y) en el plano cartesiano de las calificaciones de matemáticas y de física respectivamente. En el caso concreto el diagrama de dispersión se muestra en la figura 1
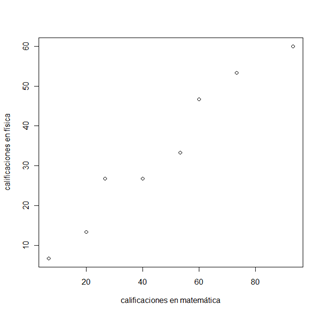
Figura 1
El gráfico refleja que hay un comportamiento de las calificaciones de matemáticas y de física de manera directa, esto es que, a mayores valores de una le corresponden mayores valores de la otra y viceversa. Adicionalmente como tendencia, se detecta un comportamiento lineal entre los valores de las calificaciones de matemáticas y de física.
-
Pero, nótese que aún con un gráfico como el que muestra la figura 2, se advierte que a mayores calificaciones en matemáticas corresponden menores calificaciones en física, es decir, que se evidencia una relación inversa o negativa de las variables, el producto de sus valores será positivo y en consecuencia su suma. Esto requiere que se modifique de alguna manera el gráfico. Se sugiere entonces colocar el centro de coordenadas, es decir el punto (0,0), en el punto (x ¯,y ¯), como se muestra en figura 3
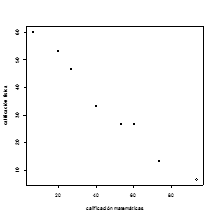
Figura 2
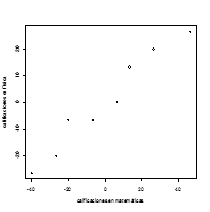
Figura 3
El efecto de centrar el diagrama de dispersión en el punto (x ¯,y ¯) se logra restando a cada valor de X y de Y la media muestral correspondiente, y luego graficar estos datos corregidos por la media en un diagrama de dispersión. En consecuencia, el producto de los valores de X y Y corregidos por su respectiva media muestral, muestra valores negativos
1064.50 , 534.24 , 132.50 , 44.22 , -0.24 , 78.22 , 531.75 , 1243.47.Pero su suma es positiva, lo cual es un índice de que prevalecen los productos positivos sobre los negativos, por lo que se concluye que la asociación lineal es positiva, y se toma como valor de esta a la suma de los productos, en este caso 3728.67. Valdría la pregunta: • ¿cuán grande es la asociación lineal entre las calificaciones de matemáticas y física?
-
Si en lugar de expresarse las calificaciones en una escala entre 0 y 100, se expresara entre 0 y 10, se obtendría un diagrama similar al obtenido en la figura 3, pero en esta ocasión la suma de los productos de las calificaciones corregidas por la media es de 37.2867, cien veces más pequeño el valor de la asociación entre las mismas dos variables, solo que ahora están expresadas en otra escala. A la luz del resultado de este análisis, todo indica que la medida de la asociación lineal que se ha intentado definir no es la más apropiada, ya que la misma está seriamente afectada por la escala de medición de las variables.
-
Procede entonces aplicar otra transformación a los datos, después de ser corregidos por sus respectivas medias muestrales, dividiendo cada uno por su respectiva desviación estándar. En este caso la suma de los productos de estos datos transformados es robusta ante cualquier escala de medición que se utilice y adicionalmente, al dividirse por la cantidad de pares de observaciones menos uno, tomará valores entre -1 y 1, se obtiene así la expresión 1, la cual corresponde a la fórmula para el cálculo del coeficiente de correlación lineal.
-
Corresponde ahora ilustrar situaciones donde el coeficiente de correlación toma valores extremos, es decir, 1, -1.
-
En el caso de que los valores de las variables fuesen los que se muestran a continuación:
Matemáticas
6.7
20.0
26.7
40.0
53.3
60.0
73.3
93.3
Física
3.35
10.0
13.35
20.0
26.65
30.0
36.65
46.65
Su diagrama de dispersión es el que se muestra en la figura 4
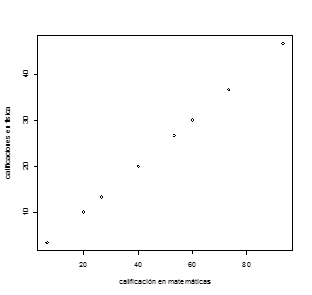
Figura 4
-
Como se aprecia en este último diagrama de dispersión, todos los puntos (x,y) descansan sobre una línea recta que indica una relación lineal directa o positiva entre los valores de las variables, la mejor de todas las que pueden existir. Es de esperar entonces que r sea igual a 1. Este resultado se debe verificar para que sirva de ilustración de cómo calcular r.
Para el cálculo manual del coeficiente de correlación se sugiere utilizar la siguiente tabla:
Var 1
Var 2
Col 3
Col 4
Col 5
Col 6
Col 7
x
y
x-mediax
y-mediay
(Col 3)2
(Col 4)2
(col 3xcol 4)
6.7
3.35
-39.9625
-19.98125
1597.00141
399.250352
798.500703
20.0
10.0
-26.6625
-13.33125
710.888906
177.722227
355.444453
26.7
13.35
-19.9625
-9.98125
398.501406
99.6253516
199.250703
40.0
20.0
-6.6625
-3.33125
44.3889063
11.0972266
22.1944531
53.3
26.65
6.6375
3.31875
44.0564062
11.0141016
22.0282031
60.0
30.0
13.3375
6.66875
177.888906
44.4722266
88.9444531
73.3
36.65
26.6375
13.31875
709.556406
177.389102
354.778203
93.3
46.65
46.6375
23.31875
2175.05641
543.764102
1087.5282
TOTAL
5857.33875
1464.33469
2928.66938
Calculando el valor de r mediante la fórmula expresada en (2) se tiene
-
Si las calificaciones fuesen ahora las siguientes:
Matemáticas
6.7
20.0
26.7
40.0
53.3
60.0
73.3
93.3
Física
44.65
38.00
34.65
28.00
21.35
18.00
11.35
1.35
El diagrama de dispersión es el que se muestra en la figura 5
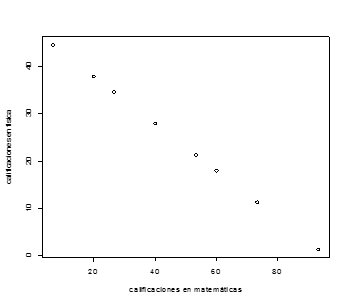
Figura 5
Se aprecia que los puntos (x,y) correspondientes a las calificaciones de matemáticas y Física descansan sobre una misma línea recta, sólo que en este caso la línea recta evidencia una relación inversa o negativa entre ambas calificaciones, esperándose entonces que el coeficiente de correlación tome el valor de -1.
Var 1
Var 2
Col 3
Col 4
Col 5
Col 6
Col 7
x
y
x-mediax
y-mediay
(Col 3)2
(Col 4)2
(col 3xcol 4)
6.7
44.65
-39.9625
19.98125
1597.00141
399.250352
-798.500703
20.0
38.00
-26.6625
13.33125
710.888906
177.722227
-355.444453
26.7
34.65
-19.9625
9.98125
398.501406
99.6253516
-199.250703
40.0
28.00
-6.6625
3.33125
44.3889063
11.0972266
-22.1944531
53.3
21.35
6.6375
-3.31875
44.0564062
11.0141016
-22.0282031
60.0
18.00
13.3375
-6.66875
177.888906
44.4722266
-88.9444531
73.3
11.35
26.6375
-13.31875
709.556406
177.389102
-354.778203
93.3
1.35
46.6375
-23.31875
2175.05641
543.764102
-1087.5282
TOTAL
5857.33875
1464.33469
-2928.66938
Por último, en la medida en que el valor del coeficiente se aleje de los valores extremos 1 y -1, la intensidad de la correlación o asociación lineal irá disminuyendo, hasta alcanzar el valor 0, lo cual significará que no existe correlación lineal entre la variables.
CONCLUSIONES
Se ha brindado un ejemplo en contexto que puede reflejar un problema de la realidad,al tomar como fuente de información los datos del ejemplo, ha sido posible obtener una expresión para cuantificar la intensidad de la asociación o relación lineal entre dos variables, a saber el coeficiente de correlación lineal de Pearson. Con la estrategia de enseñanza que se propone, no solo se obtiene la expresión de cálculo de dicho coeficiente, sino que se evidencian las propiedades de este coeficiente, así como su correcta interpretación.
REFERENCIAS BIBLIOGRÁFICAS
Aaron, A, Aaron, E, N. and Coups, E. J. (2008).Statistics for the Behavioral and Social Sciences.4thedition.Pearson Prentice Hall. USA.
Batanero, C. 2001. Didáctica de la Estadística. Grupo de Investigación en Educación Estadística. Universidad de Granada. España.
DeGroot, M. H. (1998). Probabilidad y Estadística. 2ª Edición.SITESA.México.
Everson, M., Zieffler, A. and Garfield, J. (2008).Implementing new reform guidelines in teaching introductory statistics courses. Teaching Statistics, 30(3).
Gal, I. and Ginsburg L. (1994). The role of beliefs and attitudes in learning statistics: Towards an assessment framework. Journalof Statistics Education, 2(2),
Garfield, J., Aliaga, M., Cobb, G., Cuff, C.,Gould, R., Lock, R., Moore, T., Rossman, A., Stephenson, R., Utts, J., Velleman, P. and Witmer, J. (2005). Guidelines for Assessmentand Instruction in Statistics Education(GAISE).
http://www.amstat.org/education/gaise/ (revisado 16 enero, 2007).
Guerra, C., Menéndez, E., Barrero, R. y Egaña, E. (1998). Estadística. 2ª Reimpresión.. Félix Varela. Cuba.
Mvududu, N. and. Kanyongo, G. Y. (2011).Using Real Life Examples to Teach Abstract Statistical Concepts.TeachingStatistics.Vol.33, No. 1.
Symanzik, J. and Vukasinovic, N (2006).Teaching an introductory statistics course with CyberStats, an electronic textbook. Journal of Statistics Education, 14(1).
Welsh, A. H. (1996). Aspects of Statistical Inference.Wiley. USA