INTRODUCCIÓN
Investigaciones realizadas en estudiantes que inician la universidad exhiben la existencia de dificultades derivadas del hecho de no han desarrollado la capacidad de utilizar el concepto matemático de una manera adecuada en situaciones contextualizadas, aun cuando estas formen parte de sus experiencias personales y conocimientos anteriores. La incomprensión del concepto matemático persiste desde la escuela secundaria hasta el inicio de la universidad. Los estudiantes evitan cualquier acercamiento algebraico y retornan a procedimientos de carácter aritmético(Cuesta, 2012) en especial cuando el problema implica cierto nivel de razonamiento de las situaciones y los diferentes contextos en que se presenta la tarea.
Lo anterior pone en evidencia la falta de competencia del estudiante egresado de bachillerato para expresar en lenguaje algebraico relaciones planteadas verbalmente o desde un entorno geométrico, entendiendo la competencia como “los modos en que los escolares actúan cuando hacen matemáticas y cuando se enfrentan a problemas”.(Rico, 2010)
Ahora bien, ¿mejora la competencia después de cursar matemática universitaria? Responder a esta interroganteexige organizar, comparar y analizar información a partir de las actuaciones de diferentes grupos de estudiantes universitarios, cuando se enfrentana la tarea de responder a situaciones sencillas planteadas en diversos contextos. La investigación que reportamos tuvo por objetivo caracterizar las actuaciones y las dificultades cuando el estudiante se enfrenta a la tarea de resolver problemas aritmético-algebraicosde enunciado verbal.
Se toman como referencias las ideas desarrolladas por Eugenio Filloy sobre el análisis y clasificación de actuaciones del modelo teórico local, que comprende cuatro componentes interrelacionadas: (i) el modelo de enseñanza, (ii) el modelo de procesos cognitivos, (iii) el modelo de comunicación, y (iv) el modelo de competencia formal (Filloy, 1984).
El componente de actuación o modelo de cognición constituye el marco propicio para identificar y categorizar las actuaciones de los estudiantes cuando se enfrentan a tareas contextualizadas que involucran la relación entre variables (A., C. 2007).
DESARROLLO
Con la finalidad de analizar estrategias y dificultades, se estudian las actuaciones escritas del estudiante cuando intenta determinar los valores máximo o mínimo en situaciones sencillas, no necesariamente vinculadas con los estudios de cálculo diferencialen la universidad.
Se toma una muestra de 75 estudiantes de la licenciatura en economía, representativa de tres grupos con distintos niveles académicos. Los grupos están diferenciados por el nivel de conocimientos impartido en clases sobre concepto de valor extremo (máximo y mínimo) de una función y sobre el uso de derivadas para resolver problemas de optimización. Por la evidente necesidad de mantener la confidencialidad de los estudiantes, se les asigna un código de referencia en función del grupo al que pertenecen (ver Tabla 1).
Grupo de: |
Situación al momento de la prueba: |
Número de estudiantes: |
Codificación: |
Cálculo I |
Estudia cálculo diferencial de funciones de una variable real, pero aún no ha estudiado su relación con problemas de maximización o minimización. |
25 |
I1, …, I25 |
Cálculo II |
Recientemente estudió el concepto de máximo/mínimo de una función de una variable real y la resolución de problemas de optimización con derivadas. Actualmente estudia funciones de varias variables. |
22 |
II26, …, II47 |
Econometría |
Hace un año estudió problemas de optimización,culminando con optimizaciónrestringida de funciones de varias variables por el método de los multiplicadores de Lagrange. |
28 |
E48, …, E75 |
La prueba escrita consiste en cuatro situaciones - problema en las que se solicita determinar el máximo o mínimo, para ello activa cualquier conocimiento adquirido desde la secundaria hasta la universidad. El estudiante puede utilizar diversos procedimientos, desde resolver con operaciones aritméticas elementales o con procedimientos algebraicos, hasta los métodos de optimización estudiados en los cursos universitarios. Se entrevista a una submuestrade 16 estudiantes, seleccionada bajo el criterio de que sus respuestas aporten nuevos elementos acerca de las dificultades y el modo de actuar de los estudiantes.
Procesamiento:
La lectura preliminar de las respuestas escritas permitió conocer las diferentes actuaciones de los estudiantes. Aunque serán posteriormente tratadas en el análisis de cada una de los problemas propuestos, las estrategias inferidas de las actuaciones se clasifican en las siguientes categorías:
Aritmética: Se aborda el problema con procedimientos de tipo aritmético, experimentando con valores que satisfagan las condiciones establecidas, seguido de operaciones elementales que conducen o no a una solución correcta.
Algebraica: A partir del contexto verbalmente planteado y/o de la solución aritmética se procura expresar una relación algebraica entre las cantidades desconocidas y relaciones implicadas en el problema; de la cual se podría llegar a una solución, correcta o incorrecta, por procedimientos de optimización que provienen del cálculo diferencial en una o dos variables.
Incomprensión: La actuación del estudiante manifiesta una total o parcial incomprensión del contexto del problema y/o de las condiciones y relaciones implicadas.
Cabe destacar que las categorías no son excluyentes; es decir, se encuentran casos de estudiantes que, aun desarrollando una estrategia aritmética o algebraica, manifiestan incomprensión del contexto del problema.
Problema 1:Encuentra dos números positivos y cuya suma sea , pero cuya multiplicación sea la máxima posible.
Con aritmética elemental, un gran número de estudiantes determina que tales números son y ; sin embargo, se presentan respuestas incorrectas, como resultado de una interpretación inadecuada de la situación. En efecto, algunos estudiantes no aciertan dado que, en la frase “dos números positivos y ”, interpretan que ambos números deben ser diferentes y enteros, concluyendo en consecuencia que y , o viceversa. Durante la entrevista se pregunta “¿cómo llegas a la conclusión de que los números son y ?”, y las respuestas son: “por tanteo”, “comprobando con varios cálculos” o “realizando tabla de valores”.
Los estudiantes de los grupos de Cálculo I y II tienen mayor nivel de comprensión que los estudiantes de Econometría (ver Tabla 2). Esto puede estar asociado a su cercanía temporal con los estudios preuniversitarios, en los que frecuentemente se abordan situaciones similares a la planteada con herramientas aritméticas elementales; mientras que algunos estudiantes de Econometría intentan abordar el problema con procedimientos sofisticados adquiridos en sus estudios universitarios.
Grupo: |
Porcentaje de aciertos: |
Porcentaje de alumnos que utilizan la estrategia: |
||
Aritmética |
Algebraica |
Incomprensión |
||
Cálculo I |
96 |
100 |
0 |
4 |
Cálculo II |
86.4 |
100 |
9 |
3.6 |
Econometría |
89 |
100 |
10.7 |
11 |
Durante la entrevista se pregunta “¿se puede demostrar matemáticamente que los números son y ?” o “¿se puede expresar y/o llegar a la solución de manera algebraica?”. Muchos estudiantes, aun teniendo una solución aritmética correcta, no son capaces de transferir dicho conocimiento a una expresión de tipo algebraico. Resultó que, de los 16 entrevistados, sólo un estudiante de Econometría logra plantear el problema algebraicamente. El resto de los estudiantes proporciona respuestas del tipo “no recuerdo”, “no entiendo cómo”, “sólo si asigno un valor a uno de los números” o “no sé plantearlo”, las cuáles evidencian la existencia de obstáculos para trasferir el problema, y su solución aritmética, al lenguaje algebraico.
Problema 2:Una huerta tiene actualmente árboles, que producen frutos cada uno. Se calcula que por cada árbol adicional plantado la producción de cada árbol disminuirá en frutos. ¿Cuántos árboles adicionales deben plantarse para que la producción total de la huerta sea máxima? ¿Es realista tu respuesta? De no serlo, ¿qué decidirías si fueras el dueño de la huerta?
Una situación latente es la incomprensión del enunciado y/o de las condiciones del problema (ver Tabla 3). La inmensa mayoría de los estudiantes pueden determinar que la producción total actual es de frutos (resultado al que arriban mediante la multiplicación ), pero se genera un serio conflicto que inicia con la completa incomprensión de la frase “por cada árbol adicional plantado la producción de cada árbol disminuirá en frutos” e incluye la inadecuada interpretación de la naturaleza de la dependencia de la producción total con respecto al número de árboles plantados.
Grupo: |
Porcentaje de aciertos: |
Porcentaje de alumnos que utilizan la estrategia: |
||
Aritmética |
Algebraica |
Incomprensión |
||
Cálculo I |
28 |
36 |
4 |
68 |
Cálculo II |
36.4 |
31.8 |
9.1 |
50 |
Econometría |
39.3 |
32.1 |
7.1 |
46.4 |
De esta manera, no se observa mayor nivel de comprensión del estudiante después de haber cursado dos cursos de cálculo diferencial en la universidad. En otros casos, y como resultado de una comprensión del contexto y de las condiciones del problema, la estrategia utilizada es aritmética. Durante la entrevista, solo cuatro estudiantes logran, bajo la guía del entrevistador, escribir la expresión algebraica del tipo . Para el resto resultó un serio conflicto trasladar el conocimiento que se tiene sobre el problema a su expresión algebraica, como se muestra en este fragmento de entrevista con el estudiante II34.
Profesor: ¿Cómo expresar algebraicamente los resultados aritméticos?
Estudiante II34: Con una regla de tres.
P: ¿Cómo podemos llegar al resultado con una regla de tres?
II34: Por árboles se producen frutos… Se me dificulta encontrar la cantidad.
P: Observa la primera columna de tus resultados aritméticos, estás incrementando la cantidad de árboles de uno en uno, mientras que en la segunda columna disminuyes de en . Y después multiplicas los resultados de ambas columnas. ¿Podemos de cada columna obtener una expresión matemática y luego multiplicar?
II34: Sí.
P: ¿Cómo? ¿Por qué no llamamos a la variable incrementada?
II34: No, no sé cómo hacerlo.
En otros casos, los estudiantes intentan proponer una solución de tipo algebraica, que no refleja comprensión del problema. Obsérvense en el siguiente fragmento de entrevista: primero, su incomprensión de la situación verbalmente planteada; y, posteriormente, la dificultad para trasladar el conocimiento aritmético a una expresión algebraica.
Profesor: En tu respuesta escrita, ¿qué significa ?
Estudiante E54: La cantidad de árboles adicionales, menos que disminuye por cada árbol adicional.
P: ¿Cuál sería la producción si se plantan árboles adicionales?
E54: Según yo, debe ir disminuyendo la producción.
P: Por ejemplo, ¿si se plantan árboles?
E54: Sería .
P: ¿Si se plantan ?
E54: Sería .
P: Observa que a medida que incrementas un árbol la producción disminuye en , la pregunta es, ¿cómo se puede expresar algebraicamente?
E54: Sería como… [No responde].
P: Bien, llamemos a la cantidad de árboles adicionales.
E54: [Escribe la expresión: ].
P: ¿Por qué igualas tales expresiones? Estás igualando cantidad de árboles a cantidad de frutos.
E54: [No responde].
P: Tienes que es la cantidad de árboles, ¿qué debemos hacer para obtener la producción total?
E54: Este…[Señala la expresión ]… El número de árboles.P: ¿Por qué lo debemos multiplicar?
E54: Por.
P: Muy bien, observa que la expresión [escribe ] satisface los cálculos anteriores.
E54: Sí, ya entiendo.
Problema 3: Un rectángulo tiene perímetro fijo de cm., ¿cuánto deben medir sus lados para que el área del rectángulo sea lo más grande posible?
Un gran número de estudiantes no acierta a responder (ver Tabla 4). La primera causa es, precisamente, la incomprensión del contexto geométrico, de los conceptos involucrados (perímetro y área) o de la relación existente entre ambos.
Grupo: |
Porcentaje de aciertos: |
Porcentaje de alumnos que utilizan la estrategia: |
||
Aritmética |
Algebraica |
Incomprensión |
||
Cálculo I |
8 |
56 |
0 |
44 |
Cálculo II |
4.5 |
54.5 |
4.5 |
41 |
Econometría |
11 |
60.7 |
3.6 |
64.3 |
El estudiante I2 en el siguiente fragmento de entrevista, muestra algún matiz de estrategia algebraica, a pesar de la cual prevalece el aspecto de incomprensión:
Profesora: ¿Qué no entiendes en este problema?
Estudiante I21: Es que debo checar cuánto mide cada lado, para que el perímetro sea y no recuerdo cómo hacer para sacar cada lado.
P: Tu problema es que no sabes cómo separar en cuatro valores; sin embargo, en el primer problema puedes separar en dos valores. ¿No te parece que básicamente debes hacer como en el Problema 1?
I21: Sí.
P: Pero tienes otra condición, ¿cuál es?
I21: Que el área sea lo más grande, pero no entiendo cómo.
En segundo lugar, surge de la comprensión de los conceptos de perímetro y área, no aporta una respuesta correcta debido a las concepciones del estudiante acerca de rectángulos y cuadrados. El estudiante no reconoce que los valores que maximizan el área sean y . Resulta interesante que la totalidad de los estudiantes entrevistados respondan que los valores que maximizan el área son y (o viceversa), y que durante la entrevista se responda como sigue:
Profesor: ¿No puede ser en cada uno de los lados?
Estudiante: No, porque entonces sería un cuadrado, y no un rectángulo, como se expresa en el problema.
P: ¿Qué es un rectángulo?
E: Una figura con dos pares de lados iguales, pero unos son mayores que otros, o la base mayor que la altura.
P: ¿Entonces un cuadrado es un rectángulo?
E: No, porque en el cuadrado todos los lados son iguales.
P: ¿Cómo se halla el área de un rectángulo?
E: Base por altura.
P: ¿Cómo se halla el área de un cuadrado?
E: Lado por lado.
Con independencia del grado de avance, las respuestas en los tres grupos ponen de manifiesto que no se tiene una definición correcta, al punto que algunos estudiantes no pueden responder a preguntas como: “¿Qué significa la palabra cuadrilátero?” o “¿qué significa la palabra rectángulo?”. Cabe destacar que la dificultad conceptual va acompañada de los prototipos visuales que se tiene sobre el cuadrado (“el que tiene cuatro lados iguales”) y el rectángulo (“el que tiene la base mayor que la altura”).
En resumen, se pudo comprobar que no se tiene la competencia necesaria para trasladar los resultados obtenidos (aritméticos) a expresiones algebraicas, porque se desconoce la relación existente entre los conceptos de perímetro y área, como se muestra en las respuestas de I18
Profesora: ¿Puedes representar algebraicamente las condiciones del problema?
Estudiante I18: No, me costaría mucho trabajo.
P: ¿Puedes simbolizar cada lado de la figura y tratar de expresar las condiciones?
E: [No responde].
P: Intenta expresar, primero el área y luego el perímetro.
E: Es lo complicado, si tengo valores lo puedo hacer, pero plantearlo me cuesta trabajo.
Los porcentajes de incomprensión mostrados en la Tabla 4 muestran lo complicado que resulta a los estudiantes avanzados (grupo de Econometría) entender el contexto geométrico de este problema. Al igual que en el caso del Problema 1, esto puede deberse a que, son precisamente ellos quienes se encuentran más alejados temporalmente de los cursos en los que se suelen abordar situaciones geométricas, que no son objeto de análisis en los estudios universitarios. Situación que se complica por la tendencia a utilizar herramientas sofisticadas estudiadas en la universidad que, independientemente de su pertinencia, no siempre fueron bien comprendidas. Así, cuando el nivel académico formal no ha implicado aprendizaje significativo, se transforma más bien en un obstáculo para la comprensión del contenido de los problemas y para el tránsito de los lenguajes común y aritmético al algebraico.
Problema 4: Con la finalidad de motivar a los automovilistas para que contemplen los paisajes naturales de Veracruz, la Secretaría de Turismo del Gobierno del Estado está planeando construir áreas de camping al lado de las carreteras. Cada área de camping debe ser rectangular, con una superficie de metros cuadrados (ver Figura 1). Por supuesto, el lado frontal adyacente a la carretera no debe estar cercado. ¿Cuál debe ser la longitud del lado frontal a fin de que la cantidad necesaria de malla para cercar sea mínima?
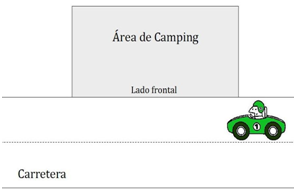
Figura 1
En la actuación de muchos estudiantes de los tres grupos (ver Tabla 5) se observa incomprensión de las condiciones verbalmente planteadas, causada por una lectura inadecuada del enunciado, y/o por el desconocimiento que se tiene sobre los conceptos implicados en la tarea.
Grupo: |
Porcentaje de aciertos: |
Porcentaje de alumnos que utilizan la estrategia: |
||
Aritmética |
Algebraica |
Incomprensión |
||
Cálculo I |
4 |
12 |
0 |
88 |
Cálculo II |
36.4 |
27.4 |
9 |
63.6 |
Econometría |
31 |
50 |
8 |
42 |
Tabla 5: Porcentajes de aciertos y de uso de estrategias en el Problema 4.
Surgen respuestas como las que aporta el estudiante I21:
Estudiante I21: Se supone que son metros cuadrados [señala la Figura 1]… el lado frontal no se debe cercar.
Profesora: No, no se puede cercar.
I21: Es un rectángulo… ¿Se puede decir que su área es de metros cuadrados?
P: Sí.
I21: No, no entiendo.
P: Observa, se desea colocar malla a estos tres lados [señala la Figura 1], pero se desea que la cantidad de malla sea la menor posible, pero el área debe ser metros cuadrados, ¿qué valores podrían ser?
I21: No sé.
P: Bien, supongamos que damos valores de al lado frontal y al lado lateral, ¿cómo calculas el perímetro?
I21: Lado por lado.
En otros casos, la actuación se limita a una operación aritmética, consistente en proponer dos valores cuya multiplicación sea , y no más; causado por la desconexión existente entre los conceptos de perímetro y área. Se pudo comprobar que 7 de los 16 estudiantes entrevistados responden, acertadamente, que el lado frontal debe ser de metros y el ortogonal de metros, pero solo dos pueden verificar (de manera aritmética) que la cantidad necesaria de malla sea mínima. Un ejemplo es la respuesta de II28.
Profesor: ¿Cómo llegas a esta respuesta?
Estudiante II28: Multiplicando con la calculadora, para que me diera tomé algunas variantes.
P: ¿Pero cómo determinas que deben ser y ?
II28: Realicé algunas variantes, incluso con números no enteros, y fui calculando la cantidad de malla. Al final llego a la conclusión que debe ser la respuesta correcta.
Bajo la guía de las preguntas formuladas en la entrevista, otros tres estudiantes logran verificar (de manera aritmética) que, efectivamente, la cantidad de malla utilizada debe ser metros, pero solo un estudiante (de Cálculo I) de los 16 entrevistados logra la expresión algebraica.
De los resultados obtenidos en este problema, tampoco se observa una mejora significativa, ni de la comprensión del problema, ni del porcentaje de estudiantes que aciertan, ni de la competencia para plantear algebraicamente la situación problema que pueda atribuirse a los cursos de matemáticas recibidos en la universidad.
CONCLUSIONES
El estudio tuvo como objetivo analizar las estrategias y competencias algebraicas de tres grupos de estudiantes universitarios con diferentes niveles de avance formal dentro de la misma licenciatura. Aun cuando la detección y análisis de dificultades de comprensión lectora no fue uno de los propósitos de investigación originalmente planteados, se constató que la primera y principal dificultad emerge precisamente de la incomprensión del enunciado o del contexto del problema; situación que varía dependiendo del nivel de complejidad de los problemas propuestos y del instrumental matemático que el estudiante considera disponible y pertinente.
En los problemas que requieren un nivel elemental de análisis (problemas 1 y 3) el estudiante menos avanzado en los estudios universitarios (de los grupos de Cálculo I o II) muestra, de manera relativa, mayor comprensión que el estudiante más avanzado (del grupo de Econometría) a causa de que: (i) el estudiante menos avanzado recuerda mejor aquello que estudió hace relativamente poco tiempo (3 o 6 meses) en los cursos preuniversitarios, y (ii) el estudiante avanzado recuerda menos e intenta utilizar herramientas sofisticadas estudiadas recientemente en la universidad que, causado por la propia incomprensión, no le permiten llegar a una solución. Contrastando con esto, en los problemas que requieren de “más conocimiento” (problemas 2 y 4), se invierten los resultados. El estudiante del grupo de Econometría obtiene mejores resultados gracias a la utilización de algunos procedimientos algebraicos estudiados en la universidad, lo cual no significa que necesariamente comprenda mejor los problemas, tan solo que se vale de más recursos de carácter procedimental.
Lo anterior hace notar que, en lo relativo al nivel de comprensión de las situaciones verbalmente planteadas, no existen diferencias significativas entre los grupos y cursar matemáticas avanzadas en la universidad no garantiza que se comprenda mejor la naturaleza de las relaciones existentes entre los datos y las incógnitas. Los cursos universitarios resultan en ocasiones contraproducentes, porque el estudiante arriba a ellos sin un conocimiento bien consolidado de la matemática elemental y sin haber desarrollado la capacidad de utilizar el nuevo conocimiento de manera flexible en situaciones o problemas que formen parte de sus experiencias personales y conocimientos anteriores. Así las cosas, el curso avanzado de matemáticas produce más confusión, acrecentando el acervo de conceptos y procedimientos mal entendidos.
De manera generalizada se utilizan estrategias y procedimientos de carácter aritmético, pero se pudo corroborar que se hace de forma instrumental y memorística, sin la competencia para transferir dicho conocimiento (sobre el contexto y su solución aritmética) a una expresión algebraica. Los estudiantes de los tres grupos recurren por igual al uso de estos procedimientos con fuente de significado limitada, que no resulta suficiente para aplicar procedimientos de generalización algebraica. En algunas situaciones (por ejemplo en el Problema 2) se genera un serio conflicto —incluso recibiendo el estudiante sugerencias del profesor— para llegar a una solución de tipo algebraica.
Con independencia de los propósitos educativos de la SEP y de la propia universidad, sehallaron relevantes indicios sobre la existencia de dificultades comunes en los tres grupos de estudiantes.Los hechos observados son:
El estudiante no posee competencia para comprender textos aritmético-algebraicos de enunciado verbal, es decir, no existe una lectura analítica del enunciado del problema que lo reduzca a una lista de cantidades y de relaciones entre cantidades, coincidiendo con lo encontrado por Filloy et al. (2008).
El nivel de conocimiento sobre el contexto geométrico es tan elemental que se desconoce incluso la relación existente entre las magnitudes (perímetro y área) a que se hace mención en algunos de los problemas.
Existen dificultades para transferir la solución aritmética del problema al lenguaje algebraico.
No se logran expresar en lenguaje algebraico relaciones planteadas verbalmente o desde el entorno geométrico y una tendencia a utilizar formalismos de tipo algebraico, descontextualizados y no comprendidos, que no son útiles al estudiante en la solución de los problemas.
REFERENCIAS BIBLIOGRÁFICAS
A., C. (2007). El proceso de aprendizaje de los conceptos de función y extremo de una función en estudiantes de economía: análisis de una innovación educativa. Barcelona, España.
Cuesta, A. y. (2012). Dificultades para comprender el concepto de variable: un estudio con estudiantes universitarios. En A. y. Cuesta, EducaciónMatemática (págs. 5-30). México: Santillana.
Filloy, Y. (1984). Proceedings of the Sixth Annual Meeting of Psychology of Mathematics Education-North America. En... y. Filloy, From an arithmetical to an algebraic thought (A clinical study with 12-13 year olds). (págs. Chapter, 1, 51-56).
Gómez, B. y. (2006). Investigación en Educación Matemática. Noveno Simposio de la Sociedad Española de Investigación en Educación Matemática SEIEM , 153-162.
Rico, L. a. (2010). Objetivos y competencias en el aprendizaje de los números naturales. En L. a. Rico, Revista Didáctica de la Matemática 54 (págs. 14-30).