UNIVERSIDAD DE MATANZAS ‘CAMILO CIENFUEGOS’

 

 

 

    CENTRO DE ESTUDIOS DE COMBUSTION Y ENERGIA

 

 

 

 

 

 

 

LAS BOMBAS DE ANILLO LIQUIDO EN LOS SISTEMAS DE VACIO DE LOS CENTRALES AZUCAREROS

 

 

 

 

MONOGRAFIA

 

 

 

AUTOR: Osvaldo Fidel García Morales.

 

 

 

 

 

 

Matanzas, Octubre de 2000.

 

 

 

 

 

 

 

 

 

INTRODUCCIÓN.

Con el triunfo de la Revolución, se han construido centrales azucareros nuevos y se han remodelado o  reconstruido muchos de los ya existentes en el país, siguiendo la política de mantener la industria azucarera como uno de los pilares fundamentales de la economía, ya que como planteara Fidel [11] " ...indiscutiblemente que podremos producir mucho más azúcar y produciremos tanto azúcar como tenga mercado, ..."

Para mantener la producción azucarera fue necesario prácticamente desde el triunfo de la Revolución, desarrollar la construcción de maquinaria azucarera, que permitiera sustituir los equipos que no se podían importar, debido al bloqueo impuesto por Estados Unidos. Muchos de estos equipos se desarrollaron a partir de prototipos importados, que no siempre se ajustaron a las necesidades reales del país. Estas condiciones obligaron a realizar estudios que permitieron mejorar los equipos, así como adecuar sus características a condiciones propias, ya que según Fidel [13]: “No se trata ya (...) del año 1959 o del año 1960, cuando empezó el bloqueo (...) y nos vimos obligados a fabricar las piezas, a inventar, a innovar, a hacer quien sabe cuántas cosas para mantener funcionando los centrales, (...). Fue un gran mérito..."

Los sistemas de vacío de los centrales azucareros son un ejemplo de la introducción paulatina de equipos producidos en el país. Las bombas de vacío de producción nacional, basadas en el principio de anillo líquido, han ido sustituyendo las viejas bombas reciprocantes que presentan grandes problemas de mantenimiento y que al ser accionadas por  máquinas de vapor reciprocantes, también son dependientes del mantenimiento de estas últimas y además conspiran contra la electrificación del central, su operatividad y fácil control.

Los diseños de las bombas de anillo líquido cubanas se han realizado a partir de prototipos del tipo NASH, adecuándolas a las características de fabricación de las empresas de producciones mecánicas nacionales, en cambio no se había hecho un estudio profundo de las capacidades necesarias, de acuerdo a las características de los sistemas de vacío en que ellas funcionaban.

Por otra parte, no se certificaba la calidad de las bombas producidas al no contar con un banco de pruebas, que permitiera medir los parámetros fundamentales de todos los tamaños, por lo que algunas bombas podían salir de la fábrica y no cumplir posteriormente su cometido.

Además no se había realizado ningún estudio del estado constructivo de estos equipos que permitiera, conjuntamente con la prueba, establecer recomendaciones para su fabricación, tendientes a mejorar su producción.

En los centrales azucareros, no siempre se realiza una reparación de los sistemas de vacío, que permita disminuir las infiltraciones hasta un valor máximo establecido, a principios de zafra. De manera que, con un razonable sobredimensionamiento, la bomba sea capaz de cubrir el incremento de la cantidad de gases incondensables, que ocurre  durante la zafra debido al deterioro normal de las instalaciones y no resulte en sobredimensionamientos excesivos como ocurre en la actualidad, en algunos centrales. También se observó que en varios centrales la temperatura del agua que alimentaba el anillo era demasiado alta, lo que conspiraba contra su capacidad y posibilidad de condensación.

Por lo general, las bombas de vacío se seleccionan con un gran sobredimensionamiento, tanto por lo explicado anteriormente, como por la falta de algunos modelos, así como por la creencia de que, mientras más grande sea la bomba mejor. En ello, también incide la falta de conciencia de ahorro en este sentido.

Trabajos realizados en la provincia de Matanzas [10,84,32] demuestran los excesos de capacidad de las bombas instaladas, así como los sobreconsumos de potencia por este concepto en un grupo de centrales, en los que se midieron las potencias consumidas por las bombas de vacío de los tachos y se calcularon las nuevas potencias, sobre la base de instalar las bombas que indica la norma ramal. Esto arrojó como resultado un sobreconsumo de potencia de 968 Kw      

Como se observa, el sobreconsumo es un valor nada despreciable, ya que su eliminación representa un ahorro de casi  nueve toneladas de combustible convencional diarios. Teniendo en cuenta todo lo anterior se han trazado los siguientes objetivos:

1) Ofrecer una metodología comprobada para la selección correcta de las bombas de vacío en el caso de los centrales azucareros.

2)Presentar una metodología de diseño de bombas de anillo líquido que permita analizar los modelos que actualmente se construyen en el país, así como diseñar y construir equipos de capacidades más acordes con las demandas de los centrales azucareros.

3) Explicar el método de ensayo de las bombas de vacío y la influencia de la temperatura del agua de enfriamiento en los parámetros energéticos de las bombas de anillo líquido.  

I.-SELECCIÓN DE CAPACIDADES

 

1.1) Tipos de bombas de vacío recomendadas para la industria azucarera:

Según  plantea Nichols [71], los criterios principales a tomarse en cuenta en el diseño de un sistema de vacío son: el tipo de proceso, la presión límite requerida (nivel de vacío), el flujo de evacuación, la temperatura a que el proceso se lleva a cabo y la sustancia a bombear. Teniendo en cuenta el flujo, la temperatura y el vacío, así como los equipos para producirlo, recomendados por Perry [79], para los centrales azucareros se tienen tres tipos de equipos: Bombas reciprocantes, eyectores y bombas de anillo líquido. Este planteamiento se puede sustentar también en los criterios manejados por Gibbs [35] y por Hull [45]. Teniendo en cuenta la sustancia a bombear, Kusay [55], Diels [23]  y Baumeister [7]plantean que cuando se van a manipular gases saturados de vapor, deben usarse bombas de anillo líquido, aspecto planteado también por Green [33], quien señala, además, que estas bombas son extremadamente confiables, bajo condiciones mínimas de operación y trabajan sin ruido ni vibraciones. Aunque señala como desventajas su gasto de agua y  potencia requerida, pone como ejemplo que el consumo de potencia en una aplicación se redujo en 50% utilizando el efecto de condensación con toberas rociadoras. Estas toberas instaladas en la tubería de succión de la bomba se alimentan con una parte del agua de sello, precondensando de esta manera el vapor saturado arrastrado por la bomba, con lo cual se reduce grandemente el volumen a manipular. Esta condición le proporciona a las bombas de anillo líquido la ventaja sobre las bombas reciprocantes y eyectores, de suplir automáticamente cualquier incremento de la capacidad del sistema, lo que se da frecuentemente en los sistemas antiguos, debido al aumento de las infiltraciones. Esto, según Cummings [21], es una gran ventaja de las bombas de anillo líquido sobre los eyectores.

Huse [44] realizó un análisis bastante amplio de la necesidad de las bombas de vacío mecánicas en la industria azucarera. y analiza varios equipos como:

Condensadores a chorro: como son de corrientes paralelas, su eficiencia es menor que la de los condensadores a contracorriente, además requieren una gran cantidad de agua para arrastrar los incondensables por fricción. Los chorros se diseñan para trabajar con una cantidad fija de agua, la cual no puede ser reducida proporcionalmente para una carga menor de operación, sin reducir su capacidad para extraer los incondensables, aumentando el consumo de agua por metro cúbico de gas incondensable a extraer.

Eyectores de vapor: Estos se usan en las fábricas azucareras con exceso de vapor (exceso de bagazo). Como se sabe esto no es práctica actual debido a los múltiples usos del bagazo. Otra desventaja estriba en que el vapor usado en ellos se contamina y no puede ser recuperado, además, si el agua se envía a un enfriadero para volver a usarla, el vapor condensado de los eyectores constituye una carga adicional de calor que aumenta la temperatura del agua del enfriadero. Los eyectores generalmente son auxiliados por otro equipo, para permitir la rápida obtención de vacío. Por esta y otras razones no se prestan para el mando automatizado, lo cual es realidad en algunos centrales y futuro en otros.

Bombas de vacío mecánicas: Estas constituyen el mejor medio para extraer los gases incondensables. Tienen la ventaja de dar buena eficiencia durante el arranque y en operación normal. Como  generalmente se acoplan a motores eléctricos, son fáciles de manipular, por tanto, son la unidad lógica para el sistema automatizado o semiautomatizado.

Es decir que el mejor sistema disponible para los evaporadores y tachos al vacío es una combinación de condensador a contracorriente  y bombas de vacío mecánicas. Esta combinación permite un bajo consumo de agua y energía.

Hugot [43]  concuerda con los aspectos planteados anteriormente, señalando además que las bombas de anillo líquido son las únicas a considerar en una nueva instalación con bombas de vacío, ya que ofrecen al mismo tiempo economía de costos inicial y de mantenimiento así como de consumo de potencia. 

Por su parte Kirk y Othmer [52] plantean que las bombas de chorros de agua se emplean comúnmente en el laboratorio, pero no a escala industrial debido al gran flujo de agua que requieren.

 

1.2) Criterios de selección de la capacidad de las bombas de vacío.

Según Cancio [9] para poder determinar qué bomba de vacío es la más adecuada para un sistema dado se necesitan dos datos fundamentales:

-Caudal de aspiración.

-Vacío requerido.

El vacío requerido se determina con el caudal y las pérdidas hidráulicas entre la bomba y el equipo al cual está conectada.

Para determinar el caudal dicho autor delimita varios casos:

1)Evacuación de un volumen.

2)Infiltraciones.

3)Gases liberados del proceso.

En el primer caso se puede utilizar la ecuación del tiempo de evacuación:

  ,[min.]                                                            (1.1)

Donde: V = Volumen del equipo, m3

            S = Caudal de bombeo, m3/h

            P1= Presión absoluta al inicio, Torr

            P2= Presión absoluta al final de la evacuación, Torr

Cuando se quiere encontrar el caudal a aspirar por la bomba se despeja S, conocidos el tiempo de evacuación y las presiones. Hay que tener en cuenta que si el caudal no es constante para los distintos grados de vacío que se consiguen con la bomba, es necesario hacer el cálculo dividiendo la curva de la bomba en zonas en las cuales el caudal sea constante, o bien que los valores de éste al principio y al final de la zona estén dentro del mismo orden de magnitud y permita obtener un valor medio. Esto también es recomendado por Spinks [90].

En el caso de equipos con funcionamiento continuo donde se presenten evacuación e infiltraciones, lo más importante son estas últimas y basta con que el caudal de la bomba sea un 10% superior al de las infiltraciones para satisfacer el proceso.

Para conocer las infiltraciones se pueden realizar  pruebas de  hermeticidad o tomar algunas de las recomendaciones dadas por los diferentes autores.

En el tercer caso, el aire liberado del proceso puede considerarse como una infiltración interior y sumarse con la exterior para determinar el caudal de aspiración. Para calcularlo se toman  recomendaciones propias del proceso en cuestión.

Según Pavielko [76], la cantidad de gases incondensables a extraer del condensador barométrico, se determina aproximadamente por la ecuación siguiente:

            ,[m3/ t.c]                                                    (1.2)

Donde : Gg= cantidad de gases incondensables, m3/t.c

                D= cantidad de vapor que condensa, % de la caña molida

                po= presión de vacío en la succión de la bomba, Torr

                to= temperatura de gases incondensables, oC.

 

Según Popov [83] el flujo volumétrico de gases a succionar es:

    ,[m3/ s]                                                        (1.3)

Donde: t= temperatura de aire en la entrada de la bomba, oC

             P1= presión del aire succionado, Pa.

              b = coeficiente experimental.

             D= flujo de vapor que condensa, Kg./s.

Por su parte Pavlov plantea que el flujo másico de aire (Gaire) a extraer se calcula como:

  Gaire= 0,00025   (W+Gag) + 0,01W, [kg/s].            (1.4)

Donde: W =  consumo de vapor secundario al condensador, kg/s.

             Gag= consumo de agua al condensador, kg/seg.

El Indice [66] establece que la capacidad de la bomba de vacío para los evaporadores debe ser de 250 pie3 /min. por cada 1000 pie2 del vaso melador (0,0762 m3/min.m2). Para los tachos 750 pie3/min. por cada 100 000 @ de caña molida (0,0187 m3/min.t.c) y 400 pie3/min. por cada 100 000 @ de caña molida (0,01 m3/min.t.c) para la bomba auxiliar.

Para el caso de la industria azucarera Hugot  [43] brinda una serie de recomendaciones importantes para determinar el caudal de aspiración de la bomba de vacío. Plantea que los gases incondensables introducidos al condensador provienen de cuatro fuentes:

1- Con el vapor de calentamiento (a1)

2- Con el jugo (a2)

3- Con el agua de inyección  (a3)

4- Por infiltraciones (a4)

1. Generalmente a1=0 porque no se comunica el vapor de calentamiento con el condensador. Si se comunica y el agua de alimentar proviene de condensados con una pequeña reposición: a1=5-10 ppm del vapor vivo o de escape usado.

2. a2= 200-250 ppm del jugo para los evaporadores.

a2= 50-100 ppm del sirope para tachos.

Los jugos de caña, a diferencia de la remolacha no dan una cantidad apreciable de amoniaco. Por otro lado, los jugos que llegan a los evaporadores ya han sido calentados y han desprendido los gases en el tanque expansionador (flash) por lo que se consideran sólo los gases disueltos entre clarificaciones y evaporaciones.

3. Para el agua de inyección proveniente de enfriadero, la cantidad de aire introducido por la misma es:

a3=30-40 ppm del flujo de agua.

4. La cantidad de aire proveniente de infiltraciones:

a4=500-2000 ppm del vapor a condensar, para tacho, buena instalación, compacta, con pocas tuberías y juntas.

a4=2000-4000 ppm del vapor a condensar para múltiple efecto con dos o tres vasos, instalación promedio.

a4=4000-8000 ppm para un número de tachos, instalación compleja, con muchas válvulas y juntas.        

Hugot [43] plantea también que, omitiendo el aire disuelto en el agua de inyección, se puede tomar la recomendación de Badger [6]  que toma los criterios de los siguientes autores para la cantidad de aire a extraer:

Weiss: 0,5% del volumen de vapor a condensar.

Corner: 0,28-0,34% del volumen de vapor a condensar en dependencia del número de efectos (0,28 para simple efecto, 0,34 para quíntuple).

Coxon: 0,25 -0,35%  del volumen de vapor a condensar, para múltiples de azúcar de caña.

Hugot [43] da la siguiente fórmula más simplificada para determinar la cantidad de aire:

Gaire=(a3. W+a') Q.           [Kg/s]               (1.5)

Donde:a3= aire proveniente del agua de inyección, Kg aire/millón de Kg de agua.

W= flujo de agua relativo al flujo de vapor. Kg agua/Kg vapor.

Q= flujo de vapor a condensar, en millones de Kg/s.

a'= a1 + a2 + a4 = aire introducido, Kg aire/millón de Kg de vapor a condensar.

Y establece, según las conclusiones de Perk [81] las siguientes magnitudes:

Cuádruple: a'=750 ppm.

Quíntuple a'=900 ppm

Tacho a'=1000 ppm

Los valores recomendados por la NASH   International Company [70] se basan en datos tomados de Hugot [43] y otros obtenidos por la ISSCT en Hawai, así como los tomados de la experiencia mundial de instalaciones de vacío. Estos valores también son recomendados por Huse [44]:

El aire y gases liberados del jugo o sirope: en evaporadores 250 ppm del jugo a evaporar; tachos para masa cocida  A y B: 100 ppm del sirope o meladura; tachos para masa cocida C: 50 ppm del sirope. Unos 30 ppm de aire y gases son introducidos por el agua de inyección. El aire proveniente de infiltraciones: 3500 ppm del vapor que condensa y para los tachos unos 400 ppm/h de la cantidad de vapor total producido en la templa.

Según la Nash [70], después de determinar el flujo másico de gases incondensables se determina el flujo volumétrico a partir de la ecuación de los gases perfectos:           

V=G.R.T/P, [m3/h]                                                                                        (1.6)

Donde: G= flujo másico a aspirar, kg/h

R= Constante del aire, 287 J/kg.K

             P= presión parcial del aire seco, Pa

             T= temperatura de la mezcla, K

Tanto la Nash [70] como Huse [44] ofrecen gráficos para cálculos rápidos de bombas de vacío en la industria azucarera y explican que:

En el caso de evaporadores, la capacidad de la bomba expresada en pie3/min. a las condiciones de entrada se obtiene en función del flujo de jugo para diferentes temperaturas del agua de inyección

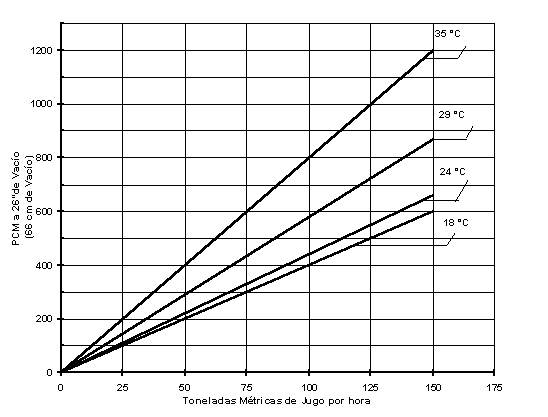
Fig.1.1 Capacidad de la bomba de vacío del evaporador.

 

 Se asumieron las siguientes condiciones: máxima velocidad de evaporación en el último efecto = 8,6 lbs/pie2.h (42,078Kg/m2.h); vacío en el último efecto = 26 Pulg. Hg(660,4 Torr); incondensables provenientes de infiltraciones = 3500 ppm del vapor producido en el último efecto; brix a la entrada del evaporador = 13; brix a la entrada del último efecto = 35; brix a la salida del evaporador = 65.

En el caso de los tachos, los incondensables a extraer son reflejados con exactitud por la superficie calórica del tacho, la cual es directamente proporcional a la velocidad de evaporación. La bomba debe ser capaz de extraer los incondensables durante las velocidades máximas de evaporación en los inicios de la templa, que es cuando la mayoría de los incondensables se libera. Las figuras 1.2, 1.3 y 1.4 muestran los requerimientos de capacidad de la bomba de vacío, expresados en función de la superficie calórica del tacho.

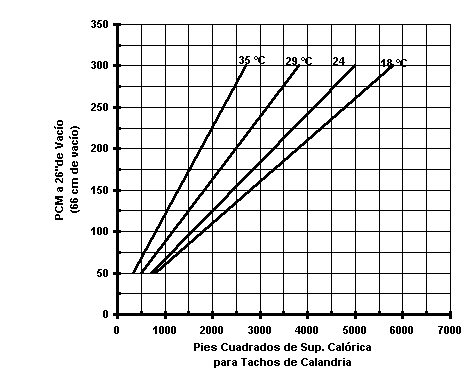
Fig. 1.2 Capacidad de la bomba de vacío de tachos A y B.

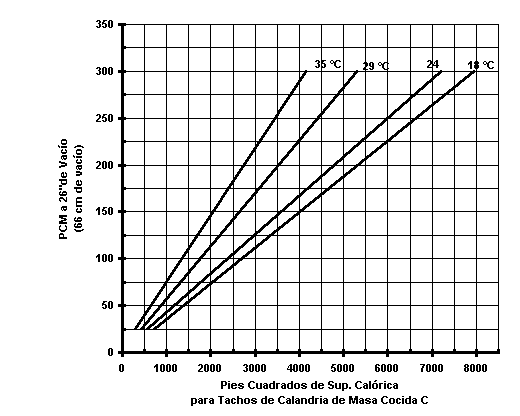
Fig. 1.3 Capacidad de la bomba de vacío para tachos C

 

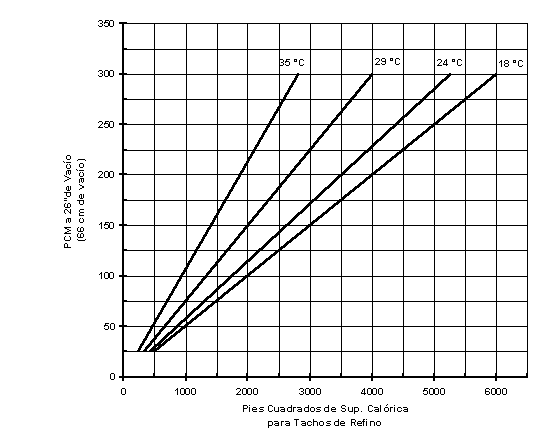
Fig. 1.4 Capacidad de la bomba de vacío para tachos de refino

Las curvas de los gráficos 1.1 al 1.4 se realizaron para 26 Pulg Hg(660.4 Torr), si se usan vacíos diferentes, los resultados deben corregirse por la tabla  1.1.

Tabla 1.1 Coeficientes de corrección de la capacidad para diferentes vacíos.

 

Temp. del agua inyección (oC)

Vacíos (Pulg Hg)

 

 

25,5

26,0

26,5

27,0

27,5

18

0,88

1

1,18

1,43

1,83

24

0,86

1

1,19

1,48

1,95

29

0,85

1

1,22

1,55

2,15

 

Estos factores se basan asumiendo que el agua de inyección y el sello de agua de la bomba tienen la misma temperatura. Si se usa agua más fresca en el sello, los factores se reducirán debido al aumento del efecto condensante de la bomba. Es decir, que la bomba actuando como un condensador auxiliar aumenta su aptitud para extraer vapores, como se observa en la siguiente tabla.

Tabla 1.2 Factores de corrección por temperatura

 

Diferencia temp. entre gases y agua de sello (ºF/ºC)

Vacío Pulg. Hg

5/2,7

10/5,5

15/8,3

20/11.1 

25,5

1,05

1,10

1,12

1,14

26,0

1,06

1,11

1,13

1,15

26,5

1,07

1,12

1,14

1,16

27,0

1,08

1,13

1,15

1,17

 

Por ejemplo, cuando la bomba está sellada con agua a temperatura de 75 oF(23,8 oC) y la temperatura de la mezcla entrante es 90 oF (32,2 oC) y el vacío 26 pulg. Hg, el factor condensante es 1,13. La bomba de vacío de anillo líquido tiene en ese caso una capacidad efectiva 1,13 veces su capacidad nominal con aire seco.

Cancio [16] también se refiere al aspecto de la condensación en la bomba. Ofrece un gráfico que permite calcular la capacidad real respecto a la nominal de la bomba de vacío de anillo líquido tipo SIHI (S/Sk), cuando aspira mezclas de aire saturadas de vapor de agua.

Cancio [16] plantea, además, que en estas bombas en los canales interálabes encerrados entre el cubo y el anillo líquido se cumple la ley de Dalton y si el aire aspirado por la bomba, no está saturado de humedad, puede llegar a saturarse totalmente debido a la evaporación del agua del anillo, reduciendo la capacidad de aspiración.

El caudal total que debe manipular la bomba (V) se obtiene:

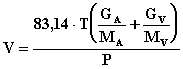,    [m3/h]                                                         (1.7)

 

Donde: T= temperatura de la mezcla, K

             P= presión total, mbar

             Ga= flujo másico de aire seco, kg/h

             Gv= flujo másico de vapor, kg/h

             Ma= masa molecular del aire, 28,9 kg/kmol

             Mv= masa molecular del vapor, 18 kg/kmol

            83,14 = constante universal de los gases perfectos,

mbar.m3/kmol.K

Paugham [75] recomienda no sobredimensionar las bombas de vacío al seleccionarlas y, además, plantea que las fugas son muy importantes.

Por otra parte, la Nash [69] ofrece gráficos con factores de condensación para diferentes temperaturas del anillo y de la mezcla de aire -vapor a manipular, para dos presiones absolutas (4 y 6 Pulg Hg) Plantea que la capacidad de la bomba puede obtenerse multiplicando la capacidad calculada por estos factores.

En el mismo trabajo [69] se muestran ejemplos de cálculos de capacidades: la infiltración en evaporadores se da con respecto al volumen total de los cuerpos al vacío como 13,33 ppm/min. Entonces, asumiendo como densidad de la meladura 90 libs/pie3 y teniendo el volumen (V) del evaporador, el flujo de infiltración (Gin) se calculará como: 

Gin = V (pie3). 90lbs/pie3 .13,33.10-6, [lbs/min]            (1.8)

Para los gases que desprende el jugo toma también 250 ppm.

En el caso del aire liberado por el agua de inyección toma la cifra de 60 ppm.

Para tachos A y B, considera la densidad de la templa como 90 lbs/pie3, el aire liberado del mismo como 1,67 ppm/min. Plantea que, aunque en realidad el aire liberado disminuye durante la templa, los cálculos se basan en requerimientos máximos. Por tanto, para calcular el flujo de gases incondensables desprendidos por la meladura (Gj) se puede usar la siguiente ecuación:

Gj = Vt .90 lbs/pie3.1, 67.10-6,  [lbs/min]           (1.9)

Donde: Vt = volumen del tacho, pie3

Para tachos de masa cocida C, recomienda un factor de 0,75. ppm/min. Los gases liberados por el agua de inyección se toman igual que para evaporadores. (60 ppm) Las infiltraciones se toman como 6,67 ppm/min.

Después de tener la suma de los tres factores se calculará el flujo volumétrico por la ecuación (1.5) de los gases perfectos.

 

1.3) Análisis de las fuentes de incondensables.

Como ya se ha explicado, existen 3 fuentes fundamentales de gases incondensables, a saber:

1- Los gases provenientes del jugo o sirope.

2- Los gases provenientes del agua de inyección.

3-Los gases provenientes de las infiltraciones.

Con respecto a la primera, varios autores coinciden en que para los jugos de caña se puede tomar 250 ppm del jugo en caso de evaporadores y entre 50 y 100 ppm de la meladura para los tachos de crudo.

En el caso de los gases provenientes del agua de inyección están los criterios coincidentes de Hugot [43], Huse [44], y la NASH [70] de recomendar entre 30 y 100 ppm del agua de inyección, preferiblemente 30 ppm cuando esta proviene de enfriadero. En cambio, también la NASH [69] recomienda tomar 60 ppm. Sin embargo, el trabajo de Ryerson [86] demostró que para trabajo normal en una estación evaporadora el flujo de gases incondensables total no sobrepasaba los 30 ppm del agua de inyección. Además, Pedroni [77] brinda un gráfico de solubilidad del aire en el agua para distintas temperaturas, en el que se observa que los 30 ppm se alcanzan a una temperatura de 10 oC, siendo menor para temperaturas mayores. Por todo lo anterior se tomará para los cálculos el valor de 30 ppm.

Como varios autores plantean y además es evidente, la tercera fuente es sobre la que más se puede actuar para disminuir la cantidad de gases incondensables, el tamaño de la bomba y los requerimientos energéticos del sistema de vacío. Tanto Yeates [97], como Rynas [87] plantean la necesidad de establecer un flujo máximo de infiltraciones como base para el diseño y mantenimiento de los equipos de vacío, ya que la magnitud del sobredimensionamiento debe tomarse cuidadosamente porque " mayor" no significa " mejor".

Ludwig [58] y Pedroni [77] explican que las infiltraciones deben medirse siempre que se pueda. Para nuevas instalaciones en proyecto recomiendan usar los valores de la figura 1.5

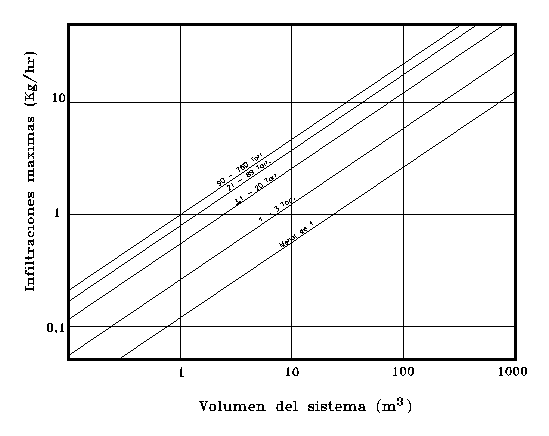
Fig. 1.5 Infiltraciones en función del volumen

Los autores explican que dichos valores son para sistemas comercialmente ajustados. Como se ve estas infiltraciones están vinculadas al volumen del sistema. Recomiendan tomar para la capacidad del equipo de vacío el doble de lo que da el gráfico, explicando que esto arroja valores muy elevados en el caso de sistemas muy voluminosos, con pocas uniones roscadas o bridadas, válvulas y accesorios y valores muy pequeños cuando se trata de equipos de volumen reducido pero con gran cantidad de uniones y accesorios. Esto es lógico pues el procedimiento tiene el defecto de no tomar en cuenta las características particulares del sistema en cuestión. En realidad las pérdidas dependen de la calidad de montaje de la instalación, espesores de junta y técnicas de apretado, eficiencia de la empaquetadura. En un sistema bien ajustado se encuentran valores de fuga 50 al 70 % de lo dado en el gráfico, en cambio si el sistema está mal ajustado o mal montado pueden encontrarse pérdidas dos o tres veces mayores.

Ludwig [58] plantea que se deben aplicar factores razonables de seguridad a cada una de las fuentes con el fin de asegurar la capacidad adecuada y recomienda para eyectores tomar un factor de sobredimensionamiento total de 1,2 a 2,0. En cambio, Pedroni [77] señala que en equipos de vacío las pérdidas son muy caras, de modo que antes que conservadores en su estimación conviene ser cuidadosos en la selección y ajuste de los accesorios.

Wallas [96] recomienda calcular la cantidad de aire infiltrado. (Gin) a una instalación bajo vacío por la siguiente expresión:

Gin = C. V 2/3, [lbs/h]                                               (1.10)

Donde: V = Volumen del equipo, pie 3.

           C = coeficiente que depende de la presión (mayor a 90 Torr se toma 0,2)

Por su parte Gómez [36] presenta un método de cálculo rápido de infiltraciones, basado en la modelación de curvas publicadas por el Heat Exchange Institute. La ecuación es:

Gin = A. V B, [Kg/h]                                                 (1.11)

Donde: V = volumen del sistema, m 3

           A y B = coeficientes que dependen de la presión (si es mayor a 90 Torr se toman

           A = 0,943 y B = 0,663)

Los resultados obtenidos por esta ecuación coinciden con los de Wallas.

Cancio [9] también recomienda medir las infiltraciones y para una instalación en proyecto da dos tipos de recomendaciones, una basada en el volumen del vacío y otra en la longitud de las juntas las cuales se pueden analizar en las siguientes tablas.

Tabla 1.3. Infiltraciones atendiendo al volumen.

Volumen instalación, (m 3)

infiltraciones, (kg/h)

0,1

0,1-0,5

1

0,5-1

3

1-2

5

2-4

10

3-6

25

4-8

50

5-10

100

8-20

200

10-30

                              

Tabla 1.4 Infiltraciones atendiendo a la junta

Calidad

Infiltraciones kg/hm de junta

muy buena

0,03

buena

0,1

normal

0,2

 

Los valores indicados son válidos para aire a 20 OC y presiones absolutas inferiores a 349,5 Torr, ya que a partir de este valor de la presión las infiltraciones permanecen constantes.

Conviene sobredimensionar los valores obtenidos por este sistema, con un factor de seguridad que la experiencia aconseja 1,5 para bombas de anillo líquido.

De lo analizado hasta aquí se puede concluir que la predicción teórica del flujo de infiltraciones es bastante imprecisa, ya que no sólo depende del volumen del sistema sino también del estado técnico del mismo, es por ello que si se desea optimizar el equipamiento requerido para garantizar el vacío, es aconsejable realizar la medición directa de las infiltraciones y al mismo tiempo evaluar la calidad del mantenimiento realizado en la instalación.

 

1.4) Determinación de infiltraciones.

Cancio [9], el Índice [66] y otros autores, realizan una explicación de los métodos utilizados para determinar en la práctica las infiltraciones, lo cual se resume a continuación:

Si en una instalación de volumen V se practica el vacío, es decir se disminuye la presión absoluta interior hasta  P1, la masa de aire M1 que queda encerrada se puede calcular por la ecuación de los gases perfectos:

 

M1 = P1.V / R. T, [Kg]                                       (1.12)

Donde: P1, Pa

            V, m3

            T, K

            R = 287 J/kgK

Si se deja caer el vacío libremente, es decir se deja incrementar la presión absoluta interior hasta P2, la masa M2 dentro de la instalación puede calcularse con la misma ecuación, en la que cambia solamente la masa y la presión, si se considera que la temperatura permanece constante por tratarse de un periodo de tiempo corto. Por tanto en dicho intervalo la masa que ha entrado puede calcularse como:

                              , [Kg]     (1.13)

Y como la masa que ha entrado es el producto del gasto G multiplicado por el tiempo t que demoró el incremento de presión, dicho gasto se determinara:

    ,  [Kg/s]     (1.14) 

Donde t, se expresa en segundos.

Este método está basado en considerar que el flujo de aire que penetra por un orificio por la acción de una diferencia de presiones que no supera las condiciones criticas es independiente del valor de la presión interior (Pint/Pext)<0,53. Si se cumple esta condición, el flujo que se infiltra será independiente del incremento de la presión interior, lo que se logra al desconectar la bomba de vacío. En este caso para determinar las infiltraciones es necesario conocer el volumen total de la instalación de vacío. En sistemas complejos, donde la determinación del volumen de la instalación resulta engorrosa y poco segura, conviene independizarse del término V, para lo cual se usa el método de introducir una entrada de aire adicional conocida. En este caso se emplea una tobera convergente que se instala en el sistema y por la cual pasará un flujo constante para condiciones críticas y que puede calcularse con la siguiente expresión:

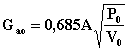   ,  [Kg/s]       (1.14)

Donde A = Area de la garganta de la tobera, m2

           Po = presión barométrica exterior, Pa

           Vo = volumen especifico  del aire exterior, m3/kg.

Para aplicar este procedimiento es necesario realizar dos corridas, la primera con la tobera incomunicada a la atmósfera y midiendo el tiempo t en que el sistema incrementa su presión en un DP prefijado; y una segunda corrida con la tobera abierta a la atmósfera, en cuyo caso el tiempo en que se alcanza el mismo DP será menor (t'<t)ya que el flujo de aire que ha penetrado G será mayor:

G = Gao + Gin, [kg./s]                                                     (1.15)

Y aplicando la ecuación (1.12) para el nuevo tiempo t’ se obtiene

    ,  [Kg/s]                                                        (1.16)

Simultaneando (2.12 y 2.15):

  ,    [Kg/s]                                                          (1.17)

Como se aprecia, la ecuación 1.17 es independiente del volumen del sistema, es decir que se puede determinar la cantidad de aire que penetra en el sistema realizando una medición con la tobera abierta a la atmósfera y otra con la tobera tapada y en ambos casos midiendo el tiempo en que se alcanza el mismo DP (t' y t respectivamente)

Las dimensiones de las toberas se toman en proporción al volumen aproximado del sistema según el Índice [66] Como se puede concluir de lo anteriormente expuesto, la evaluación de las infiltraciones reales no requiere de grandes inversiones, ya que sólo se necesita  la construcción de la tobera y como instrumentación de una columna manométrica de mercurio para medir el vacío y un cronómetro para medir el tiempo.

 

1.4.1) Resultados experimentales:

Utilizando el método de la tobera se realizó una serie de 10 mediciones durante la zafra de 1992 en un período de 46 días, en el evaporador de un central de mediana capacidad de la provincia de Matanzas [56], lo cual permitió establecer el carácter de la variación de las infiltraciones durante la zafra.

Los resultados de las mediciones se ofrecen en la tabla 1.5.

Tabla 1.5 Infiltraciones medidas en el evaporador.

Medición

Fecha

t (s)

t'(s)

Ga  (kg/h)

1

7/2/92

146

451

199

2

11/2/92

144

452

194

3

12/2/92

140

430

200,7

4

17/2/92

134

404

206,4

5

23/2/92

130

389

208,5

6

23/2/92

132

394

208,5

7

6/3/92

129

684

210,3

8

12/3/92

125

372

210,4

9

18/3/92

120

350

216,9

10

24/3/92

115

334

218,3

 

Estos resultados se procesaron, obteniéndose un modelo lineal, a partir del cual se puede trazar una estrategia de operación de los equipos de vacío. Tanto esto como las implicaciones energéticas del incremento de las infiltraciones se pueden analizar en un trabajo del autor [26].

Durante la zafra del 93 se realizaron mediciones de infiltraciones en una estación de tachos [64] por el método del volumen conocido. En este caso se dejó caer el vacío en 127 Torr (5pulg.hg), cuyos resultados se muestran a continuación:

 

Tabla 1.6. Infiltraciones individuales en tachos.

Tacho

Volumen (m3)

Tiempo (s)

Infiltración (kg./h)

1

51,6

1920

18,57

2

62,84

795

54,46

3

60,92

992

41,47

4

61,04

1440

28,44

5

66,94

1314

35,73

 

 

 1.4.2) Análisis de los resultados.

Para analizar los resultados obtenidos se puede tener en cuenta lo que plantea el Índice [66] acerca de las infiltraciones especificas:

0,325 - 0,48 Kg/hm3 Instalaciones buenas.

0,48 -  0,80 Kg/hm3 Instalaciones regulares.

0,80 -  1,28 Kg/hm3 Instalaciones malas.

También la Norma Ramal [73] establece la pérdida máxima de vacío permitida para una instalación, durante una prueba de 15 minutos de acuerdo a su volumen. Estos mismos valores aparecen en el Manual de Operaciones [93]. Teniendo en cuenta los valores extremos de esa tabla se puede establecer que las infiltraciones específicas máximas permitidas oscilan entre 0,204 - 0,424 Kg/hm3.

Las infiltraciones específicas medidas en tachos fueron:

T I  0,36 Kg/hm3

T II 0,86 Kg/hm3

T III 0,68 Kg/hm3

T IV  0,46 Kg/hm3

T V   0,52 Kg/hm3

Como se observa, sólo el tacho I se encuentra con un índice inferior al valor máximo permitido, aunque también el IV clasifica como bueno de acuerdo al Índice, el III y el V clasifican como regulares y el II como malo.

De las mediciones y resultados obtenidos en tachos se puede concluir que los valores de infiltraciones específicas máximas permitidas son alcanzables y se corresponden con los valores dados por la NASH [69,70] y por la norma para seleccionar las bombas de vacío para tachos.

Para analizar el caso del evaporador sin tener necesidad de recurrir al cálculo del volumen total, puede calcularse la infiltración específica a través de la ecuación ya vista (1.15), en la forma:

 

 ,  [Kg/hm3]                                                         (1.18)

 Después se compara el resultado con los valores establecidos.

Aplicando dicho procedimiento a las mediciones realizadas en el evaporador, se puede concluir que sobrepasa los valores de infiltraciones máximas establecidas con un gran margen. Siendo el menor valor de 2,1 Kg/hm3.

Mediciones realizadas en ese evaporador durante la misma zafra permitieron determinar el flujo de vapor que va al condensador, cuyo promedio fue de 12,4 t/h, por lo que se pudo determinar la relación infiltración/flujo de vapor, obteniéndose un valor de 16720 ppm; es decir un valor muy superior al establecido por la NASH [70]. No obstante si se analiza que el valor recomendado es 3500 ppm del vapor que va al condensador, en este caso sería, como promedio 43,4 Kg./h, es decir se reduciría a una quinta parte, lo que reduciría en la misma medida las infiltraciones específicas, alcanzando los valores máximos permitidos.

Por otra parte, resultados obtenidos en evaporadores mejor conservados como el del central "René Fraga", han demostrado que están por debajo del límite máximo permitido de infiltraciones, por lo que se puede concluir que dichos valores son alcanzables y que puede aplicarse la norma para la selección de la bomba de vacío.

 

1.5) Análisis de capacidades instaladas.

1.5.1) Metodología para el cálculo.

Todo lo analizado en los acápites anteriores de este capítulo, permite plantear la metodología para la determinación de los gases incondensables a extraer de un evaporador y de una estación de tachos. El método y los resultados obtenidos para un grupo de centrales de la provincia de Matanzas fueron publicado por el autor [25].

La cantidad de gases a extraer de un evaporador (Ae) se calcula como:

Ae = a2. J + a3. W + a4. E, [g/h]                                   (1.19).

Donde:

a2= aire y gases introducidos por el jugo, 250 ppm.

J= Flujo de jugo a evaporar, t/h.

a3= aire y gases introducidos por el agua de inyección, 30 ppm.

W= Flujo de agua de inyección, t/h.

a4= aire introducido por infiltraciones, 3500 ppm.

E= Evaporación del último efecto, t/h.

En el caso de los tachos la ecuación es:

At = a2. r mel.Vt + a3.W + a4.r mel.Vt, [g/h]                      (1.20).

Donde: a3 y W se toman igual que para evaporadores.

a2= aire y gases introducidos por la meladura, 100 ppm/h para tachos A y B, 50 ppm/h para tachos C.

r mel=densidad de la meladura, 1,44 t/m3 según NASH [69].

Vt = volumen de trabajo del tacho, m3.

a4=aire introducido por infiltraciones, 400 ppm/h.

El flujo de agua de inyección se calcula por un balance másico y térmico del condensador, en función del flujo de vapor.

El flujo de vapor que condensa en el caso de evaporadores, se calcula en función de las concentraciones y del flujo de jugo. En caso de no poseer todos los datos se puede tomar en función del área de la superficie calórica del último efecto como 41,5 Kg/hm2, según la NASH [70], que también recomienda tomar las evaporaciones en tachos según el tipo de masa cocida, como se muestra en la tabla 1.7.

Tabla 1.7 Evaporaciones en tachos.

Tipo  templa

Evapor. máxima (Kg/hm2)

Evapora. media (Kg/hm2).

   Pie

83

 

 A y B

68,3

39,0

   C

39

19,5

Esta metodología es la que sirve de base a la norma para el cálculo de selección de las bombas de vacío, así como de sus motores de accionamiento.

 

1.5.2) Discusión de resultados.

Durante la zafra de 1994 se realizó un estudio [32] en 12 centrales de la provincia de Matanzas, que permitió calcular las bombas de vacío y sus motores según la norma, así como medir el consumo de potencia de las bombas instaladas. Los resultados muestran un sobredimensionamiento, que origina un sobreconsumo de potencia de casi 1000 Kw.

Las bombas de todas las estaciones evaporadoras se recalcularon por dos métodos: Siguiendo la norma y tomando una infiltración promedio de 0,325 Kg/hm3 de volumen al vacío, arrojando resultados similares en ambos casos y que coinciden con lo publicado anteriormente[25] para las mismas estaciones. Se observa un sobredimensionamiento en la mayoría de los casos, que trae aparejado un sobreconsumo de potencia de las bombas instaladas de 535 Kw

La situación anterior está dada por la variedad de criterios para la selección, el mal estado de las reparaciones en algunos casos, así como el incremento de las infiltraciones durante el periodo de zafra y la falta de algunos modelos de bombas para cubrir todas las necesidades.

Teniendo en cuenta los factores señalados se puede recomendar que siempre que se cumplan los valores de hermeticidad establecidos por la Norma de prueba y ajuste [73], se puede aplicar la norma de selección de bombas de vacío. En caso de no cumplirse los valores de hermeticidad por ser un sistema muy complicado, podrá hacerse una medición con orificio calibrado(tobera o cámara con orificios) para establecer el flujo de infiltraciones.

Realizar las pruebas de hermeticidad periódicas durante la zafra que permitan eliminar las fugas mayores y establecer la curva de incremento normal de las infiltraciones con el objetivo de trazar estrategias de operación.

Producir en Cuba dos modelos de bombas que no se producen en la actualidad, es decir, las de tamaño 700(17m3/min=600 pie3/min) y 3000 (68 m3/min=2400 pie3/min)dado por la necesidad de su uso en algunos centrales.

 

1.5.3) Análisis económico por la introducción de la bomba 3000.

Es necesario señalar que para este análisis se consideró al MINAZ como un sistema, por lo que se analizaron los beneficios a partir de la diferencia de consumos entre las bombas 4000 y 3000. Los costos se analizaron a partir de lo que significa introducir en la EMPROMEC Primero de Mayo la producción de la bomba 3000, ya que si en la actualidad un central necesita una bomba 3000(2100 pie3/min) tiene que usar una 4000(3000 pie3/min).

El beneficio por diferencia de consumo de energía representa 5 029 $/zafra para una bomba.

El gasto de salario de la inversión asciende a $ 12 236, 80.

El gasto de material $ 2 058, 44.

El gasto de energía $ 731, 52.

Si se considera que la plantilla tiene una vida útil de 10 años y que al final no tiene valor residual. Siendo la depreciación constante en el tiempo (1502,70 $/año).

Si se realiza una producción anual de cinco bombas 3000, las cuales reportarán beneficios en el mismo año de ser producidas y a los cinco años se dedica la producción a la reposición de las primeras cinco, que ya finalizaron su vida útil y así sucesivamente en los cuatro años restantes del período de vida de la plantilla; el flujo de efectivos se puede escribir de la siguiente manera:

 

 

 

 

 

 

 

 

 

 


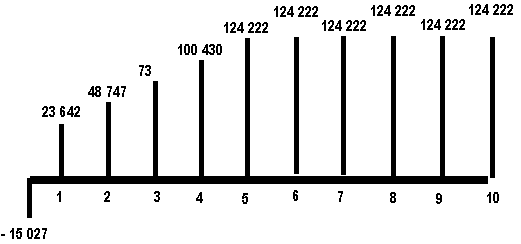
Se observa que la inversión es ventajosa ya que se paga en el primer año de vida.

El cálculo del valor actual neto del flujo de efectivos se realizó considerando una tasa de interés del 20 % y arrojó un valor de $ 328 963.

El cálculo de la tasa interna de retorno (TIR) demostró que la inversión se justifica para cualquier costo de capital.

 

 

1.5.4) Efecto económico por disminución del sobredimensionamiento.

Como fue explicado anteriormente, debido al sobredimensionamiento de las capacidades existentes, en los centrales azucareros de la provincia de Matanzas que se analizaron, estaban instalados adicionalmente 1503 KW de potencia, lo cual representa un sobreconsumo de 3 607 200 KWh de energía/zafra, es decir el consumo de energía anual de 2004 viviendas  modestamente equipadas (150 KWh/mes) o $ 229 057/zafra.

Este efecto podría obtenerse a partir de la sustitución paulatina de dichas bombas, en la medida en que vayan alcanzando el fin de su vida útil y sea por tanto, imprescindible su cambio, lo cual reduciría al mínimo las inversiones a realizar.

 

II: DISEÑO

2.1) Estudio bibliográfico

Este aspecto ha sido muy poco tratado en la literatura y  aunque hay algunos autores que ofrecen relaciones para los parámetros fundamentales de funcionamiento, en función de las características constructivas, la única metodología que se conoce para el diseño es la publicada por Pfleyderer [80].

Kovats [54] da una explicación de las bombas de aire usadas en el cebado de las bombas centrífugas, explicando que existen dos tipos: rotatorias de anillo líquido y de canal lateral.

Plantea que las primeras son excéntricas, mostrando un gráfico simplificado como el siguiente:

 

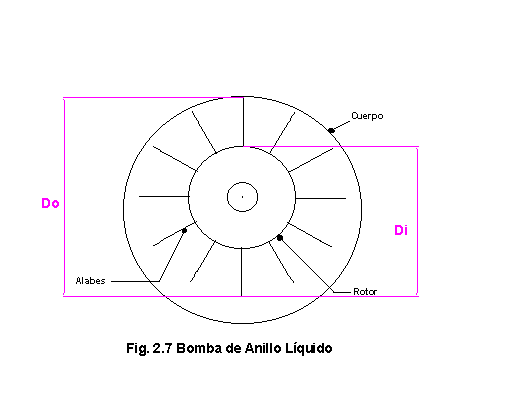
La velocidad periférica del agua puede calcularse como:

      ,[m/s]                                                          (2.1)

Donde: Do = Diámetro exterior del impelente, m.

              n = frecuencia de rotación del impelente min-1

              Di = diámetro interior del anillo líquido, m.

La excentricidad se puede calcular como:

   ,[m]                                                                         (2.2)

La capacidad de la bomba se calcula:

      [m3/s]                                              (2.3)

Donde: b = ancho de la bomba, m.

                hv = (0,8-0,9) rendimiento volumétrico de la bomba.

La velocidad periférica mínima necesaria para comprimir el aire desde la presión Ho hasta Hat, en m.c.a es:

  , [m2/s2]                                                          (2.4)

Por su parte Cherkasski [18] plantea que el caudal que manipula la bomba se calcula como:

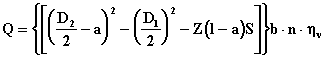,  [m3/s]             (2.5)

Donde: D2 y D1 = diámetros exterior e interior del rodete, m

                       a = inmersión mínima del álabe en el anillo de agua; m

                       Z, = cantidad de álabes;

                       l = longitud radial del álabe a (D2- D1)/2; m

                      S= espesor de los álabes, m

                       b = ancho de los álabes, m

                       n = la frecuencia de rotación; s-1

                        hv  = rendimiento volumétrico (0,96.)

Una expresión similar la brinda Chlumsky [20]

Pfleiderer [80] realiza una profunda explicación teórica acerca del funcionamiento de la bomba de anillo líquido, llegando a demostrar las principales expresiones para su cálculo de diseño. Los aspectos fundamentales serán resumidos a continuación:

2.1.2) Principio de funcionamiento.

La bomba de anillo de agua consiste en un rodete provisto de álabes dirigidos en forma radial y situados en un cuerpo cilíndrico parcialmente lleno de agua en posición  excéntrica, como se muestra en la siguiente fig.2.2

 

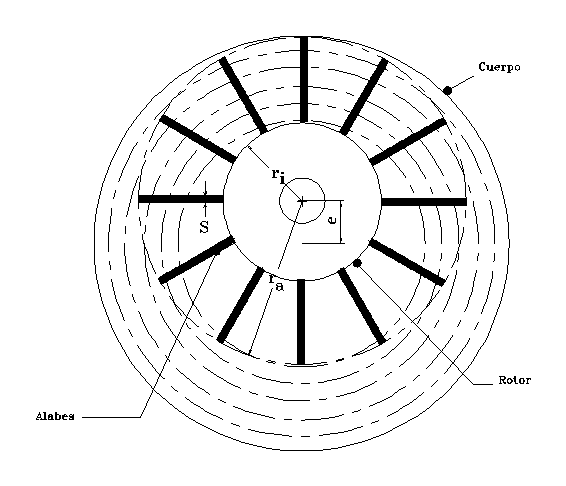
Fig. 2.2 Principales Parámetros geométricos de la bomba de vacío

 

Al girar el rodete, se forma un anillo de agua y los álabes quedan encerrados por los lados formando una serie de cámaras o espacios vacíos producto a que se adosan a las paredes del cuerpo con un juego reducido.

Debido a la posición excéntrica del rodete, los álabes al girar penetran en el anillo de agua de modo que la parte libre de agua de las  celdas durante una revolución aumentan primero de tamaño para después reducirse, produciéndose un efecto de aspiración primero y  un efecto de compresión  o un efecto de elevación a través de la abertura de impulsión.

Es indispensable que las superficies laterales del rodete ajusten bien contra las paredes laterales planas del cuerpo de la bomba, en los cuales se encuentran las aberturas de aspiración e impulsión, puesto que de otra forma se producirán grandes pérdidas por fugas.

El cierre periférico queda asegurado por el anillo de agua. Por lo general, esta bomba es menos susceptible a las impurezas del líquido a elevar.

En las bombas de anillo de agua anchas, sería difícil llenar rápidamente los espacios entre los álabes si sólo existieran aberturas en un solo lado; por este motivo es conveniente proveer en ambos lados aberturas de aspiración e impulsión, es decir construir la bomba con doble succión.

2.1.3) Particularidades de su construcción.

Relativo a los detalles constructivos de la bomba de anillo líquido resulta ventajoso construir el cuerpo, no como un cilindro circular, sino dotado de una o varias expansiones. Asimismo, los álabes no se distribuyen generalmente en forma radial, sino curvados hacia adelante.

2.1.4) La presión de suministro.

Se demuestra que existe una relación de presiones máxima alcanzable, es decir:

                                                              (2.6)

Donde: l = es un coeficiente de velocidades que tiene en cuenta

               el adelanto de los álabes y es muy cercano a la unidad.

               h1 y h2 = presiones de succión y descarga respectivamente,

               mm de agua.

               E = es el grado de rapidez que se expresa por:

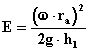                                                                                    (2.7)

Donde: w = velocidad angular, s-1.

              ra  radio exterior, m.

De lo anterior se obtiene como velocidad tangencial mínima posible:

             ,[m/s]                                  (2.8)

Esta expresión es muy adecuada para obtener la frecuencia necesaria para alcanzar una presión dada. El ángulo de comienzo del orificio de descarga (j) correspondiente a la condición anterior se puede calcular mediante el valor de A, que se obtiene de:

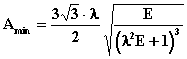                                                           (2.9)

Y se sustituye en la siguiente expresión para determinar el valor de h

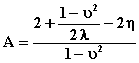                                                                       (2.10)

Para lo cual es necesario asumir un valor de la relación de radios n =ri/ra. El ángulo entonces podrá determinarse de la siguiente expresión de h 

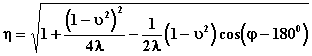                            (2.11)

2.15) Limitación interna del anillo de agua.

Para el lado de presión se demuestra que:

                                                                     (2.12)

Donde: ry = valor del radio hasta el que penetra el agua en dicho lado.

En la que sustituyendo el valor de  Xmax:

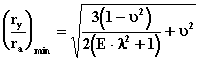                                                        (2.13)

Y para el lado de aspiración:

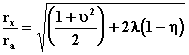                                                           (2.14)

Donde rx = valor del radio del agua para dicho lado.

2.1.6)Posición inclinada del nivel de agua. Número de álabes.

A causa de la aceleración que los álabes provocan en el agua, en cada celda se tiene una posición inclinada del nivel de agua. Esta posición inclinada no debe alcanzar el espacio en forma de arco, porque entonces se rompería el sello de agua y el aire escaparía. Esto da origen a que exista un número mínimo de álabes que cumplan esta condición.

Los cálculos demuestran que la mayor inclinación ocurre en el lado de aspiración a unos treinta grados después del punto muerto superior y en el lado de presión, al alcanzar la presión máxima. Sin embargo en estos puntos la penetración de los álabes en el anillo es tan grande que no existe ningún peligro de perder la estanqueidad. El peligro se presenta más fácilmente en los puntos en que la penetración es pequeña (cerca del punto muerto inferior) por lo que se recomienda poner en este punto una penetración adicional "A" como seguridad, a no ser que se quiera disponer de más álabes de los necesarios.

 

2.1.7) Forma de los orificios de aspiración e impulsión.

En rigor, el orificio de aspiración debería extenderse a casi todo el lado derecho de la bomba. El orificio de presión debe empezar exactamente en el ángulo j, donde según el cálculo se ha alcanzado la relación de presión deseada. La limitación interior del anillo de agua a lo largo del orificio de presión, es similar a la obtenida para el lado de aspiración, teniendo en cuenta que la velocidad es otra, lo cual puede obtenerse como:

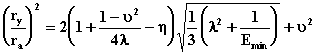                                    (2.15)

Pudiendo dibujarse a través de ella, la limitación interior del anillo de agua, variando j. La limitación exterior del orificio de impulsión  deberá seguir la forma de la limitación interior del anillo de agua en dicho lado, pero a una distancia de la misma que mantenga la penetración "A" deseada en el punto muerto inferior de la bomba.

En cuanto al orificio de aspiración, la forma de la superficie del anillo de agua, fijada según la ecuación ya vista para ese lado, da solamente un límite máximo, que no es necesario alcanzar por existir espacio suficiente para situar la superficie de paso indispensable.

 

2.1.8)  Consideración de los espesores de pared y juegos laterales.

En la bomba real, los álabes tienen espesor finito "s" siendo también conveniente una cierta inmersión "A" de los álabes.

Si no existieran huelgos entre las superficies frontales del cubo y de los álabes del rodete, a través de los cuales se produce una fuga de aire de la parte de presión a la de aspiración y si no existiera ninguna disminución de presión entre el punto de medición, en la tubería de aspiración y  el interior de la bomba en el lado de aspiración; el volumen de gases aspirado sería:

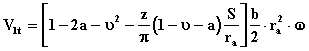          ,[m3/s]         (2.16)

Donde a = A/ra, inmersión relativa de los álabes.

Si se considerase las fugas y las resistencias de aspiración mediante la introducción de un rendimiento volumétrico hv  el volumen aspirado realmente sería:

V1 = hv. V1t        , [m3/s]                                                                    (2.17)

Debiéndose hallar experimentalmente. el valor de hv 

La profundidad de inmersión y el espesor de los álabes tienen poca influencia sobre la altura de presión alcanzable.

 

2.1.9) Potencia útil y rendimiento.

La potencia útil de la bomba en kg.m/s, suponiendo la compresión isotérmica será:

      ,[Kg.m/s]    (2.18)

Donde P2 y P1 en kgf/m2 o h2 y h1 en metros de agua representan las presiones de salida y entrada de la bomba.

El aire aspirado tiene gran humedad debido al agua auxiliar y a la temperatura elevada de ésta. El grado de saturación es aproximadamente 100%. Se debe tener en cuenta que para P1 o h1 se toman las presiones parciales del aire seco  puesto que el vapor de agua se condensa con un aumento isotérmico de la presión. Esto es de interés cuando las presiones de aspiración son pequeñas como es el caso de las bombas de vacío.

 

 

2.2) Metodología de diseño

2.2.1) Introducción:

En Cuba se construyen las bombas de vacío de anillo líquido desde hace algún tiempo, adaptando a las características de fabricación de las empresas de producciones mecánicas, algunos  prototipos importados; sin embargo no se había realizado un estudio profundo de la metodología de cálculo, que permitiera analizar las características de funcionamiento en aras de mejorar el diseño. La metodología de cálculo de estas bombas es un tema poco tratado en la literatura, el análisis más completo lo ofrece Pfleiderer [80], realizando una profunda explicación teórica de cada uno de los aspectos, así como la demostración de las expresiones de cálculo fundamentales. Sin embargo esta es una metodología general que sirve lo mismo para bombas de vacío como para compresores de anillo líquido, por tanto, cuando el ingeniero se enfrenta al diseño o análisis de estas bombas se encuentra que le faltan algunas recomendaciones que tienen que ver con el tipo específico de bomba. Tampoco está muy claro el método para la determinación del ángulo de comienzo del orificio de impulsión y el gráfico que ofrece Pfleiderer [80] no se ajusta a las relaciones de compresión que alcanzan las bombas de alto vacío. Con el objetivo de ofrecer una metodología más completa y que pueda ser utilizada tanto por los ingenieros de la producción como por las empresas dedicadas a la construcción de bombas de vacío se realizó un análisis de la bibliografía y se estudiaron los equipos existentes, así como las informaciones brindadas por distintos fabricantes.

Los resultados alcanzados se muestran en este epígrafe, donde se ofrecen las expresiones y algunos criterios prácticos del autor para determinar los principales parámetros de estas bombas.

 

2.2.2)Metodología.

Anteriormente se hizo un resumen del tratado teórico realizado por Pfleiderer [80] sobre las bombas de anillo líquido, por tanto en este epígrafe sólo se expondrán los pasos necesarios para realizar los cálculos de diseño, precisando algunos coeficientes.

Para el diseño se deben tener como datos de entrada el flujo volumétrico a aspirar por la bomba(V1) y las presiones de aspiración (h1) e impulsión (h2).

 

1)Cálculo de la potencia al eje:

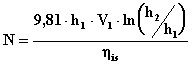     , [KW]                                     (2.19)

Donde: h1 = presión parcial del aire seco en la aspiración, m.c.a.

             h2 = Presión absoluta en la descarga, m.c.a.

             V1 = Flujo volumétrico total aspirado por la bomba, m3/s.

his = Rendimiento energético o de acoplamiento de la bomba, oscila alrededor de 0,20 para bombas tipo NASH [30] para un vacío de 27 pulg. de Hg (685 Torr), succionando aire seco a 20 oC y trabajando con agua de enfriamiento a 15 oC. Este rendimiento decrece rápidamente al incrementarse la temperatura del agua de enfriamiento [30, 31].

2) Cálculo de la velocidad tangencial mínima del rodete; según la ecuación 2.8:

 

,          [m/s]                                        (2.20)

Donde l es la relación de velocidades que puede tomarse (0,88- 0,84), disminuyendo con el tamaño de la bomba.

 

3) Cálculo del ángulo de comienzo del orificio de descarga (j ):

a)Primeramente se determina el grado de rapidez(Emin), a través de la ecuación 2.7:

 

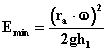                                                                                      (2.21)

b)Posteriormente se determina el valor de Amin, por la ecuación 2.9:

 

                                                   (2.22)

Se sustituye en E el valor de Emin. calculado.

 

c)Cálculo del valor de  h . Despejando de la ecuación 2.10:

                                                                   (2.23)

Se sustituye en A el valor de Amin calculado.

Se puede asumir n =0,456-0,371.

d)Cálculo de  j :Despejando de la ecuación 2.11:

 

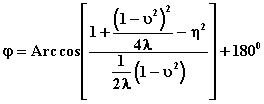                                               (2.24)

4)Suposición de los valores de:

a)Número de álabes (Z): Las bombas cubanas se construyen generalmente de 16 álabes.

b)Espesor relativo de los álabes (s/ra): En las bombas cubanas este oscila entre 0,063 y 0,044.

c) Inmersión relativa de los álabes (a =A/ra): Puede tomarse como un 2%.

d) Frecuencia de rotación (n): Se recomienda tomar los valores de las bombas tipo NASH de capacidades similares [30], mostrados en la tabla 2.1

Tabla 2.1 Valores de frecuencia de rotación recomendados para bombas de vacío

CAPACIDAD(pie3/min)

FRECUENCIA(r.p.m.)

5000

330

3000

400

2000

500

1500

590

800

820

550

1050

325

1320

O valores similares para guardar la relación apropiada que debe existir entre el ancho (b) y el radio exterior del rodete(b/ra), ya que las bombas muy anchas no se llenan rápidamente y desaprovechan su capacidad.

e)Rendimiento volumétrico(ηv): Para las bomba  tipo NASH puede tomarse (0,65-0,7); aunque, según, estudios teóricos realizados por el autor [31] puede disminuir hasta 0,45 cuando la temperatura del agua de enfriamiento alcanza 35 oC.

5)Cálculo de las dimensiones fundamentales de la bomba:

a)Si la bomba es de doble succión, el ancho de cada parte por el radio exterior (b.ra) se calculará, despejando de la ecuación 2.16, como:

 

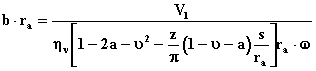       , [m2]                (2.25)

b)Cálculo del radio exterior(ra):

 

    , [m]                                                                             (2.26)

También se puede tomar la relación b/ra = 0,85 para calcular el valor del radio exterior (ra), como:

 

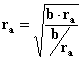        , [m]                                                                             (2.27)

Entonces podrá determinarse el valor de la frecuencia de rotación mínima.

c) Cálculo del ancho (b):

b = b.ra/ra       , [m]                                                                                        (2.28)

d) Cálculo del radio interior (ri):

ri = n.ra,   , [m]                                                                                         (2.29)

e) Cálculo del espesor (s);

s = s/ra.ra    , [m]                                                                                       (2.30)

 

6) Cálculo de las limitaciones exteriores de los orificios de presión y aspiración:

a) Orificio de aspiración. Según la ecuación 2.14:

 

       ,[m]                                                      (2.31)

b) Orificio de descarga:

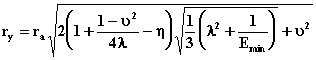          ,[m]                  (2.32)

En la práctica de construcción de bombas en Cuba, los valores de rx son (7-14)% inferiores y los de ry (17-29)% inferiores.

 

2.2.3) Validación de la metodología.

Con el objetivo de realizar una comprobación del grado en que se ajusta la metodología, a los valores reales de diseño de las bombas cubanas, se calcularon tres modelos de ellas: 4003 (3000 pie3/min), 2003 (1500 pie3/min), 1003 (800 pie3/min); a través del programa Pascal “Disbal”, confeccionado al efecto Varios de los principales parámetros constructivos, a saber: espesor medio de los álabes (S), radios exterior e interior del rodete (ra y ri), longitud axial del impelente (b), y ángulo de comienzo del agujero de impulsión (j) se muestran en el anexo 1.

Como se puede observar los valores calculados difieren bastante poco de los valores reales de diseño, ya que la variación no sobrepasa en ningún caso el cinco por ciento.

 

2.3) Influencia de la desviación de los parámetros geométricos de diseño:

Un estudio del estado constructivo de bombas de vacío de anillo líquido [28], producidas arrojó diversas desviaciones de sus parámetros geométricos de diseño. Se analizará a continuación la influencia de dos de estos parámetros en el funcionamiento de la bomba.

2.3.1) Influencia de la variación del espesor de los álabes:

Ya que estas bombas son de doble succión, teniendo el impelente dividido en dos partes iguales (anexo 1), para cada parte se realizaron las mismas mediciones, es decir a ambos lados de la pared divisoria del impelente y en los extremos del mismo. Además, como los álabes no mantienen su espesor en todo su radio se midió el interior y el exterior, para ambas partes. Las medidas se realizaron con un pie de rey. Para mostrar los resultados se seguirá la nomenclatura siguiente:

-La medida superior corresponde con el valor del espesor en el radio interior del álabe, mientras que la inferior con el valor en el radio exterior.

-S significa espesor.

-El subíndice " i" significa en el interior (al lado de la pared divisoria del impelente)

-El subíndice "e" significa en el exterior(uno de los extremos del impelente).

-El subíndice "m" significa parte del impelente del lado del motor.

-El subíndice "o" significa parte del impelente del otro lado.

Se mostrarán los valores promediados para las cuatro bombas 2003 analizadas y los valores de los planos:

 

Tabla 2.2: Espesores de álabes bomba 2003

Parámetro

Resultados

Planos

Sim

19,3/21,4

18/22

Sio

18,9/21,8

18/22

Sem

18,9/22,8

18/22

Seo

19,5/23,0

18/22

 

Tanto los resultados de las mediciones como los de los planos fueron promediados por separado para determinar el valor medio del espesor de los álabes. Con estos valores y a partir de la ecuación 2,26 se calcularon los flujos volumétricos que se muestran (pie3/min):

Según resultados                Según planos

 1424,09                                1530,65

Se observa una diferencia de 7%, lo cual no es un valor muy grande, ya que los sobredimensionamientos se toman en ese orden. No obstante, estos sobredimensionamientos provocan desbalances en el rotor que deben ser eliminados posteriormente, así como sobreconsumo de materiales, lo cual encarece los costos de producción.

 

2.3.2) Influencia de la variación del ángulo de comienzo del orificio de descarga.

Las ecuaciones (2.21-2.24), que permiten determinar el ángulo de comienzo del orificio de descarga, muestran su dependencia de los radios interior y exterior, la frecuencia de rotación y el coeficiente de velocidades ( l), a través del grado de rapidez (E) y el valor de h.

Este ángulo se mide sobre el cono y a partir de la línea donde se mide la excentricidad del rodete respecto al cuerpo, o sea a 45 grados de la vertical y siguiendo el sentido de giro de la bomba. Las mediciones se realizaron con un goniómetro desde la línea vertical hacia ambos lados, obteniéndose después por  suma de ángulos el valor real del ángulo de comienzo del orificio de descarga.

En las cuatro bombas 2003 medidas dicho ángulo tenía un valor de 295 grados, es decir cinco grados mayor que el de diseño. Sin embargo, los cálculos realizados para este tamaño de bomba, tomando constantes sus parámetros constructivos demuestran que el ángulo debe variar con el vacío y, según los valores de la siguiente tabla:

Tabla 2.3: Valores de j en función del vacío

Vacíos

Ángulo

(Torr/pulg. Hg)

(grados)

685,8/27

290,6

660,4/26

284,2

635/25

278,2

609,6/24

272,5

584,2/23

267,2

A continuación se muestran los valores del grado de rapidez Emin, h y j para distintos valores de la frecuencia de rotación y para los valores fijos de presión de succión y descarga y radios exterior e interior.

                             Tabla 2.4:Valores de j en función de la frecuencia.

r.p.m.

450

500

650

590

620

Emin

10,94

13,52

16,48

18,8

20,77

    h

1,11

1,134

1,155

1,171

1,22

    j

284,0

286,8

289,3

290,9

294,8

Como se observa, el ángulo de comienzo del orificio de descarga de diseño (j =290 0) se corresponde con el valor de la frecuencia de rotación de trabajo, es decir n=590 r.p.m.; sin embargo la desviación del ángulo hasta 295 0 provoca que para alcanzar el mismo vacío la bomba tendría que girar a una frecuencia superior a las 620 r.p.m.

Las pruebas realizadas a estas bombas  en el banco, muestran que el vacío alcanzado fue de 25,7 pulg. Hg como promedio, es decir en ninguna se alcanzó el valor del vacío de diseño, lo cual corrobora la importancia de garantizar este ángulo en el proceso de fabricación de la bomba. El efecto económico de esta desviación puede verse a través de la influencia del vacío, en el consumo de vapor de una estación de evaporación-cocción de los centrales azucareros.

Trabajar con vacío empeorado en un evaporador, provoca un incremento en la cantidad de agua a evaporar en tachos y por tanto de la cantidad de vapor a consumir en los mismos, pudiéndose cuantificar en 0,61% por tonelada de caña el incremento del consumo de bagazo, como fue demostrado por el autor[28]. Esto representa para un central de 100t/h de molida, un sobreconsumo de 1464 t de bagazo por zafra, es decir $ 24 156, 00/zafra

La inversión a realizar para la corrección de dicho ángulo es mínima, por cuanto presupone solamente poner especial cuidado en el proceso de moldeo del cono, para que salga del taller de fundición con la lumbrera de impulsión en la posición adecuada, ya que dicho agujero no sufre un posterior maquinado.

 

III: EVALUACION

3.1) Revisión bibliográfica sobre instalaciones experimentales.

Para realizar el ensayo de la bomba de vacío debe construirse un banco de pruebas; sin embargo, en el país no existía ninguno, ni norma cubana al respecto. Por esta razón fue necesario recurrir a la experiencia internacional.

Van Atta [94], explica como pueden hacerse las mediciones en bombas mecánicas mostrando el esquema de la figura 3.1:

 

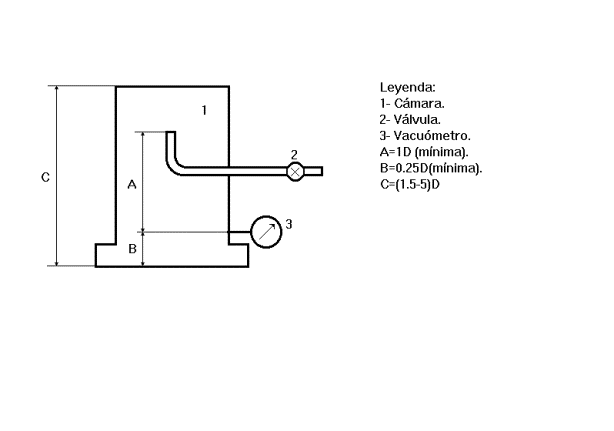
Fig. 3.1: Cámara de Van Atta.

 

Este esquema de cámara es para entradas mayores de 50 mm, para entradas menores muestra otro tipo. El diámetro de la cámara se toma igual al diámetro de entrada de la bomba.

Plantea que para medir el vacío en el rango de 1 a 760 Torr se usan manómetros de mercurio.

Para medir el flujo, cuando éste es mayor que 0,56 m3/min se emplean orificios estándar de radio largo, preferiblemente en el rango de flujo crítico.

Guthrie [38] presenta un esquema similar al ya visto, planteando que el diámetro de la cámara debe ser mayor que el de la entrada de la bomba y la altura 1,5 veces el diámetro de la cámara. Explica las formas más comunes de medición del flujo: capilar calibrado, bureta, etc.

Una norma ASME [4] explica las definiciones fundamentales señalando los parámetros a medir con sus rangos de precisión, brinda el esquema de instalación mostrado en la fig. 3.2:

 

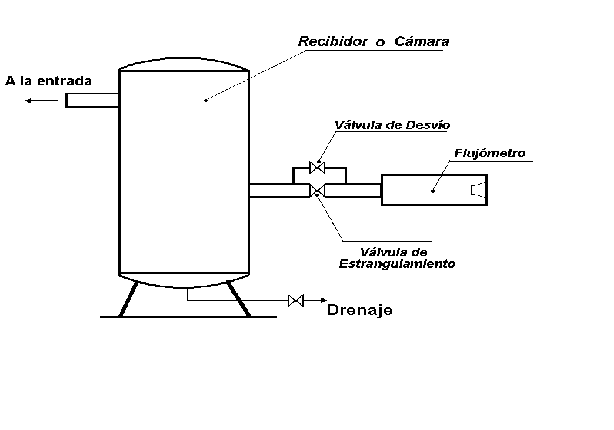
Fig. 3.2: Cámara ASME.

Una norma japonesa [48] muestra un esquema similar al de Van Atta [94], señalando que los medidores de flujo y de vacío no deben tener errores mayores del 5% y que el volumen de la cámara de pruebas debe ser al menos dos veces el volumen manipulado en una carrera de succión.

Otras normas [15,37,46] presentan esquemas similares. La diferencia de ellas con respecto al esquema está en el diámetro de la cámara que no es igual al de entrada de la bomba.

Pipko [82] presenta un esquema similar al de Van Atta señalando que la cámara debe tener un volumen cinco veces superior al manipulado en una carrera de succión. Señala que uno de los métodos para obtener la velocidad de bombeo es conocido como el método de presión constante. Por el cual la cámara de prueba se evacua y posteriormente se va dejando entrar el gas hasta las presiones definidas midiéndose el flujo por uno de los métodos conocidos. Es decir que la presión en la cámara se ajusta a diferentes valores con la ayuda de la entrada de flujo, midiéndose éste. De esta manera se puede obtener un gráfico de flujo en función de la presión de entrada.

Por su parte Chilvers [19], presenta un método sencillo y confiable de medición de las características de las bombas de vacío, basado en una serie de platos orificios que trabajan en condición crítica. Presenta el esquema de cámara de la fig. 3.3:

 

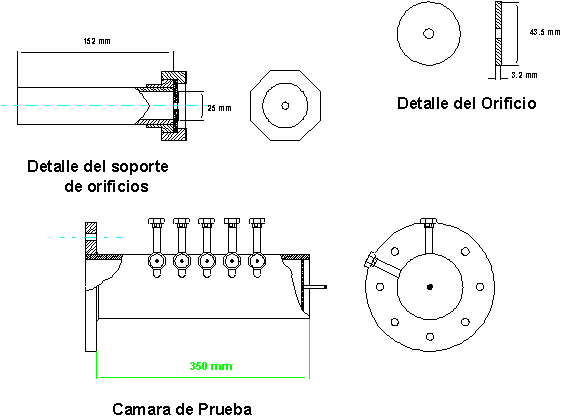
Fig. 3.3: Cámara de Chilvers.

 

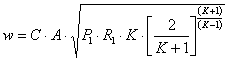
Explica que los orificios trabajan en condición crítica cuando la relación de las presiones es 52,8% para el aire y que en ese caso el flujo es máximo y se puede calcular por la  ecuación 3.1

                     (3.1)

Donde : C: Es el coeficiente de descarga.

 A  : Area de la sección transversal, m2.

 P1 : Presión absoluta a la entrada del orificio, Pa.

 R1 : Densidad del aire a la entrada, Kg/m3

K : Coeficiente adiabático.

3.2)Cámaras de pruebas y ecuaciones fundamentales.

Siguiendo las recomendaciones de Chilvers se diseñaron las cámaras a utilizar para analizar el comportamiento de las Bombas de Vacío de Anillo líquido en la EMPROMEC 1ro de  Mayo, las que se componen de un tubo central, que en su parte superior presentan una toma roscada para la colocación del vacuómetro y al cual están soldados 10 tubos con sus respectivos platos orificios, cuyos diámetros aparecen en la tabla 3.1.

Tabla 3.1 Diámetros de los platos orificios para cada tipo de bomba.

Bomba 1500

Bomba 800

Orificio   (mm)   

Orificio            (mm)    

1                 5.5  

1                          4      

2                 6

2                          5   

3                 9

3                          6  

4                 10

4                          7 

5                 12

5                          9

6                 12

6                          10

7                 12  

7                          10 

8                 12 

8                          10

9                 12     

9                          10  

10               12    

10                         10        

 

Debido  a que para el aire K = 1.4 y la relación crítica de presión: 0,528.

Se puede simplificar la ecuación 3.1 de la siguiente forma:

                         (3.2)

Sin embargo, debido a que para las bombas de vacío, lo que interesa no es el flujo másico sino el volumétrico (Q2) se puede plantear que:

                                                   (3.3)

 Donde : Q2: Flujo volumétrico, m3/s

          R2 : Densidad del aire de la cámara Kg/m3

                                              (3.4)

Donde: P2: Presión absoluta en la cámara, Pa.

Asumiendo que la temperatura se mantenga constante se sustituye 3.4 en 3.3 y ambas en 3.1 de lo cual se obtiene:

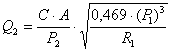                  (3.5)

Donde :

 C : (0.806 - 0.824) Se tomó para los cálculos C = 0.82 según Chilvers

A : Area de la sección de los platos orificios (mm2)

P1 = 1,013.105 Pa

T = 27 oC.

R1 = 1.178 Kg/m3

Sustituyendo los valores en la ecuación (3.5) y considerando C=0,82 constante

                                       (3.6)

Ecuación a partir de la cual puede obtenerse el flujo volumétrico (m3/min)  manipulado por cada lado de la bomba a partir del área de los platos orificios (mm2) abiertos y la presión absoluta (Kpa) existente en la cámara de pruebas.

3.3) Procedimiento de ensayo.

Se coloca la bomba en el banco de prueba, se colocan las cámaras de prueba y se atornillan a las bridas de las tapas. Posteriormente se conecta el motor de la bomba de alimentar y cuando el agua alcanza el nivel requerido se conecta el motor de la bomba de vacío, dejando que la misma comience a levantar vacío con todos los orificios  de la cámara de prueba tapados.

Al transcurrir un tiempo aproximado de 20 min. de mantenerse el vacío se procede a destapar orificios para que la bomba comience a manipular flujo, anotando para cada combinación la lectura de presión.

3.3.1 Ejemplo de resultados de pruebas.

Las mediciones tabuladas corresponden a valores promedios ya que se repitió la prueba tres veces para cada una de las combinaciones correspondientes. Con los valores que se muestran en las tablas 3.2 y 3.3 se construyeron las curvas para cada cámara, a partir de las cuales se obtuvieron las curvas generales.

Tabla 3.2: Cámara Izquierda

Pvacío

(Pulg Hg)

Pabs

(kpa)

Combinación

Area

(mm2)

Flujo

(m3/min)

Flujo

(Pie3/min)

28.4

4.72

1+2

52.01

11.03

389.4

27.7

7.37

1+2+3

115.6

15.7

554.3

26.3

12.01

1+2+3+4

194.1

16.17

571.1

24.5

18.1

1+2+3+4+5

307.1

16.96

599.6

23.9

20.15

1+2+3+6+7

341.68

16.95

596.7

23.3

22.2

1+2+6+7+8

391.1

17.63

622.57

22.4

24.2

1+2+3+4+5+6

420.14

17.37

613.15

22.1

26.2

6+7+8+9

452.16

17.27

609.8

 

Tabla 3.3 Cámara derecha

Pvacío

(Pulg Hg)

Pabs

(KPa)

Combinación

Area

FLUJO

(m3/min)

(Pie3/min)

 

28.1

5.94

1+2

52.01

8.76

309.42

27.52

7.98

1+2+3

115.6

14.5

512

26.68

10.83

1+2+3+4

194.1

17.93

633.3

24.53

8.1

1+2+3+4+5

307.1

16.98

600

24.53

18.1

1+2+3+6+7

341.68

18.85

665.6

23.3

22.2

1+2+6+7+8

391.1

17.63

622,2

22.74

24.2

1+2+3+4+5+6

420.14

17.37

613.15

22.1

26.2

6+7+8

452.16

17.27

609.8

 

 

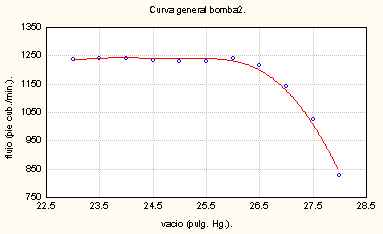
Fig. 3.4: Curva característica de bomba BVR 1500

3.4) Análisis de los resultados

Se observa que la curva característica general de la bomba tiene un comportamiento bastante cercano al del modelo original, sobre todo en su forma, ya que manipula el mayor flujo entre las 23.5 y las 25 Pulg Hg, lo cual se acerca bastante a los datos de catálogo del prototipo Nash. En cuanto a la magnitud de flujo manipulado en el punto de trabajo principal, aquí  influye el hecho de que el agua de sello en este caso posee una temperatura de 26 oC aproximadamente, mientras que para la Nash sus catálogos corresponden a temperaturas de 15 oC para el agua de sello. Esta influencia se analizará en epígrafes posteriores.

La incertidumbre experimental determinada para la presión de vacío es de 9,64 Torr, lo que constituye el 1,6%  del valor notable de 24 Pulg. Hg. En el caso del flujo la incertidumbre es 38 pie3/min, o sea el 6,4%,  pero puede reducirse realizando un número mayor de mediciones, que pudiera ser cinco por cada valor de la presión.

 

3.5) Influencia de la temperatura del agua de enfriamiento

3.5.1) Introducción

En Cuba, con un clima tropical, las temperaturas del agua disponible para el enfriamiento de los equipos energéticos son generalmente altas y los sistemas de enfriamiento empleados en los centrales azucareros son poco eficientes. Por estas razones los equipos que trabajan con sistemas de enfriamiento por agua, trabajan alejados de las zonas de explotación recomendadas por los fabricantes.

Las bombas de vacío de anillo líquido no son una excepción, y el incremento de la temperatura del agua de sello afecta sensiblemente su capacidad. A este fenómeno no se le da la suficiente importancia durante la explotación, sin embargo parece ser una de las razones que justifican el sobredimensionamiento de la capacidad instalada.

El trabajo [32] realizado, en los centrales de la provincia de Matanzas, permitió conocer que de un total de 15 bombas analizadas, sólo cinco trabajaban con agua de enfriamiento con una temperatura inferior a 30 oC y las restantes a temperaturas cercanas a los 40 oC.

Aunque existen en la literatura algunos artículos referentes a este fenómeno[19,92], y algunos fabricantes ofrecen curvas de variación del comportamiento de sus equipos con la temperatura del agua de enfriamiento, otros autores señalan que estos datos no pueden ser generalizados y que cada bomba tiene un comportamiento característico.

Todos los fabricantes de bombas de vacío de anillo líquido consultados ofrecen sus curvas características, especificando las condiciones a las cuales se realizaron las mismas. Generalmente, aire atmosférico a 20 °C y con temperatura del agua de enfriamiento a 15 °C, señalando que en caso de utilizarse agua más fría la capacidad de la bomba se incrementará, por lo que debe utilizarse el agua más fría disponible.

Como es de suponer por el principio de funcionamiento de estas bombas, cuando la temperatura del agua de enfriamiento se eleva, aumentando la presión parcial de vapor de agua en los canales interálabes y por tanto disminuyendo la presión parcial de aire seco, la capacidad de aspiración disminuye.

Cancio [9] explica que en el espacio formado entre el cubo del impulsor  y el anillo del agua en los canales interálabes, se cumple en toda su extensión la ley de Dalton y basado en ello brinda la ecuación para calcular la capacidad de la bomba, a una temperatura de líquido de servicio diferente a la que fue probada.

                                                                                                         (3.7)

Donde: St = capacidad a una temperatura t.,  (m3/min)

             S15 = capacidad a una temperatura de 15 °C,  (m3/min)

             Pvt = presión parcial de vapor a una temperatura t,  (KPa)

             Pv15 = presión parcial de vapor a 15 °C,  (KPa)

             Ptot = presión total absoluta,  (KPa)

En cambio, Chilvers [19], ofrece varios factores para el cálculo de la capacidad de la bomba en función de la temperatura del agua, los cuales difieren de los calculados por la ley de Dalton.

Explica que los factores de disminución de la capacidad dependen del diseño específico de la bomba usada, ya que existen regiones dentro de la bomba con bajas presiones, donde ocurre la autoevaporación antes de que se alcance en la entrada de la bomba el vacío teórico máximo.

Por su parte, Bacaranda [5] plantea que la temperatura del fluido interno determina una parte de sus características y Karassik [51] que requieren más potencia, comparadas con otras bombas de vacío mecánicas, debido principalmente al calentamiento del agua de circulación.

Otras investigaciones sobre el funcionamiento de las bombas de anillo líquido no refieren la influencia de la temperatura en su comportamiento [92,63,61,60,59,34]

Como en Cuba se producen bombas de vacío de anillo líquido y aunque su diseño es similar al de algunas firmas conocidas, no existe una caracterización de su comportamiento con la temperatura del agua de enfriamiento y es evidente que su conocimiento redundará en beneficio de una mejor explotación de estos equipos.

Para este análisis se diseñó y construyó una instalación experimental a escala de  laboratorio, en la que se montó una bomba importada de menor tamaño pero de similar diseño de 325 pie3/min de capacidad nominal (9.2 m3/min) a 26 Pulg Hg (660,4 Torr) de vacío.

En esta instalación se realizaron corridas experimentales en las cuales se varió la temperatura desde 27,8 hasta 42,3 oC y se evaluó su efecto en la capacidad, potencia, rendimiento y consumo específico para distintas presiones de vacío que oscilaron entre 75 y 85 Kpa (22 a 25 pulg.Hg)

3.5.2) Diseño de instalación experimental y procedimiento de ensayo.

Con el objetivo de analizar la influencia de la temperatura del agua de enfriamiento, en el funcionamiento de la bomba de vacío de anillo líquido, se construyó una instalación como la que se muestra en la fig. 3.5:

 

 

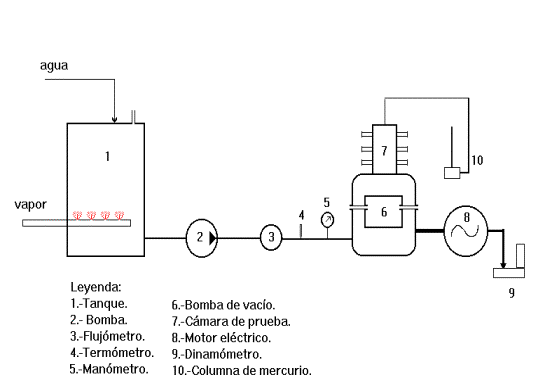
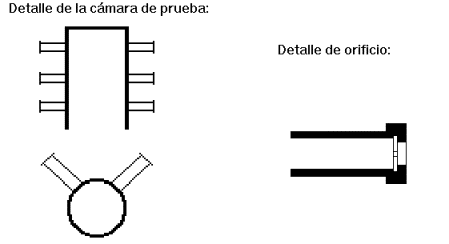
Figura 3.5: Esquema de la instalación experimental.

 

Como se observa el agua de enfriamiento se calienta en el tanque a partir de la condensación del vapor que se inyecta dentro del mismo, proveniente de una caldera. El agua es enviada por una bomba centrífuga Vida 4 a la bomba de vacío de tipo NASH CL403, a través de una tubería, donde se encuentra colocado un contador volumétrico y una válvula, que permiten controlar el flujo de agua de enfriamiento.

Un termómetro de líquido en vidrio, permite medir la temperatura así como mantenerla constante con la ayuda del control de flujo de vapor.

El manómetro de tipo Bourdon, instalado a la entrada de la bomba de vacío, permite medir la presión del agua.

La presión de la bomba de vacío se mide con una columna manométrica de mercurio, conectada al extremo cerrado de la cámara de pruebas, cuyo otro extremo se encuentra unido por bridas a una unión en T, que la conecta con las dos bocas de succión de la bomba de vacío.

La cámara de pruebas se construyó según Chilvers [19] y está constituida por un tubo central de 100 mm de diámetro, al que se encuentran soldados seis tubos de 25 mm de diámetro y 152 mm de longitud, en cuyos extremos libres se han colocado sendos platos orificios. Sus diámetros de agujero y áreas de paso se dan en la siguiente tabla.

Tabla 5.1: Platos orificios.

No

Diámetro(mm)

Area(mm2)

1,2,3

9,525

71,22

 4

6,0

28,26

 5

4,3

14,51

 6

2,5

4,9

A través de un instrumental verificador K505, conectado al motor eléctrico se pueden medir la corriente, el voltaje y la potencia consumida. Como el motor se encuentra montado en cojinetes; con la ayuda de una barra atornillada a su estator y un dinamómetro, se puede medir la fuerza para determinar el torque entregado. La frecuencia de rotación se midió con un tacómetro cronométrico.

El procedimiento empleado para realizar la prueba de la bomba, consistió en fijar la temperatura y flujo de agua y arrancar la misma con todos los orificios cerrados con tapones de goma y medir el vacío formado en la cámara. Posteriormente se iban destapando orificios y midiéndose el vacío y todos los demás parámetros en cada caso. Este procedimiento se repitió tres veces para cada medición de la presión, según plantea la Norma ISO [46].

 

3.6)Análisis de los resultados experimentales

3.6.1 Influencia de la variación de la temperatura en la capacidad de la bomba.

1) Al variar la temperatura del agua del sello, se notó una marcada influencia en la capacidad de bombeo. Como se puede observar del gráfico de la fig. 5.5, la capacidad de la bomba disminuye al aumentar la temperatura del agua.

2) Por razones atribuibles al estado técnico de la bomba, el vacío máximo alcanzado (cero gasto) no excedió los 86 Kpa (25,4 pulg. Hg), no obstante, se aprecia una disminución de este valor con el incremento de la temperatura del agua en todo el diapasón de trabajo.

3) Se aprecia un cambio en la pendiente de las curvas de capacidad para todas las temperaturas para un valor próximo a los 2,5 m3/min. No obstante las pendientes para cada temperatura son similares.

 

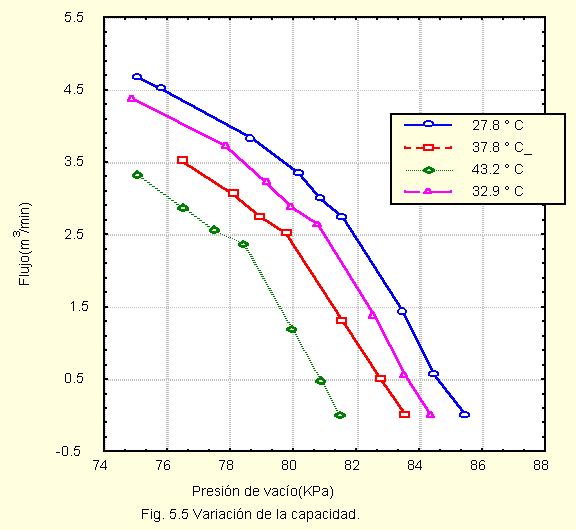
3.6.2. Influencia de la temperatura en la potencia

Para mostrar esta influencia en la potencia al eje de la bomba, se tomaron solamente los valores extremos del rango de temperatura (27.8 y 43,2 oC). Como se observa en la fig. 5.6, ésta disminuye al aumentar la temperatura, lo cual concuerda con la correspondiente disminución de la capacidad de la bomba. De forma similar se comporta la potencia consumida por el motor eléctrico.

 

 

 

 

 

 

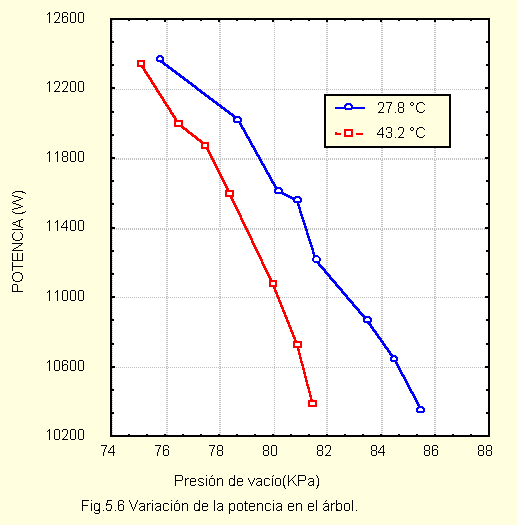
3.6.3. Influencia de la temperatura en el rendimiento de la bomba

El rendimiento isotérmico de la bomba, también presenta una característica descendiente con la presión de vacío y la temperatura. Como se aprecia en la fig. 5.8 para el intervalo de presiones ensayadas, existe aproximadamente una disminución del 10% del rendimiento para los valores extremos de temperatura.

 

 

 

 

 

 

 

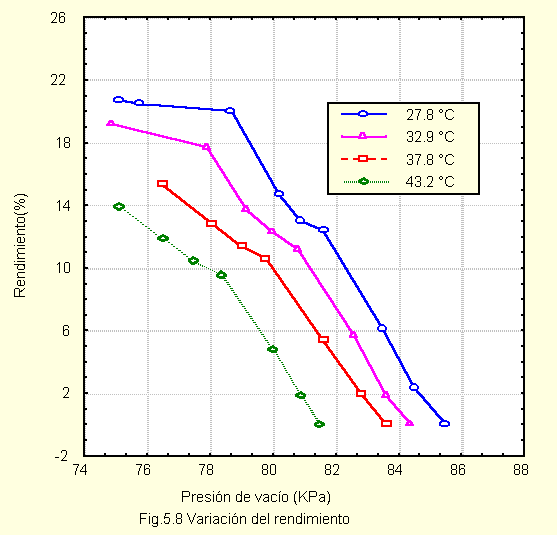
3.6.4. Influencia de la temperatura en el consumo específico de energía.

El consumo específico de energía (Kwh/m3) representa la cantidad de electricidad que consume la bomba, por cada m3 de aire bombeado. Como demuestra el gráfico de la fig. 5.9, este consumo aumenta de forma brusca con el incremento de la presión de vacío. El punto de cambio de pendiente ocurre a menores presiones de vacío a medida que aumenta la temperatura. Es notable el incremento en el consumo de energía para cada m3 bombeado para una presión dada, cuando aumenta la temperatura.

 

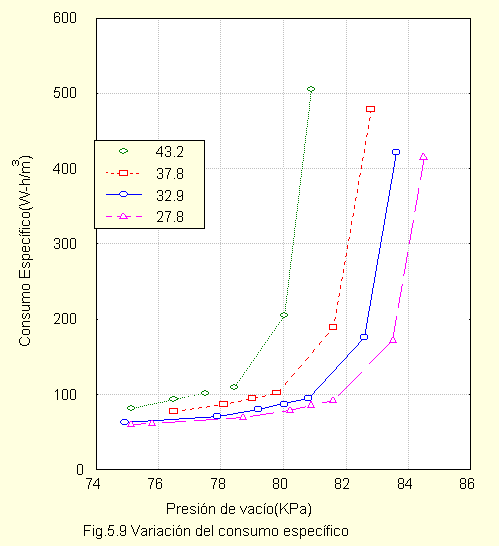
3.7) Análisis económico por la inversión del enfriadero.

Como demuestran los resultados experimentales la disminución de la temperatura del agua de sello de 37,8 a 32,9 oC provoca una disminución del consumo específico de energía de 150 W-h/m3. Esto representa para una zafra, para una bomba de 3000 pie3/min con capacidad reducida a 2905 pie3/min un consumo de 1 045 800 KW-h/zafra, es decir 66 408 $/zafra.

El costo del enfriadero y las bombas asciende a $ 45 000.

Las bombas del enfriadero gastan 27 840 KW-h/zafra =1 767,74 $/zafra.

El costo de mantenimiento del enfriadero y las bombas asciende a 147,92 $/zafra.

Suponiendo que la vida útil del enfriadero es de diez años y que al final no tiene valor residual y suponiendo una depreciación constante en el tiempo.

Conociendo que el costo de operación antes y después de la inversión se mantiene constante; el flujo de efectivos se podrá expresar como:

60 000
 

60 000
 

60 000
 

60 000
 
 


-

 

 

 

 

 


Se observa que la inversión es muy ventajosa, pagándose en el primer año de vida. El cálculo de la tasa interna de retorno demuestra que la inversión es rentable para cualquier costo de capital.

En cuatro de los centrales que trabajaban con temperaturas de agua de enfriamiento cercanas a 40 oC, las bombas de anillo líquido instaladas manipulan 283 m3/min. = 16980 m3/h = 40 752 000 m3/zafra. Por tanto, la disminución de la temperatura del agua de enfriamiento hasta valores aproximados a 33 oC, puede acarrear una disminución del consumo de energía de 6 112 800 KWh/zafra. Es decir, 388 162 $ /zafra.

REFERENCIAS BIBLOGRÁFICAS.

 

1-Adams, H.E, Liquid Ring Compressors - Some Thermodynamic Characteristics, Tappi, V 36, N 5 May 1953 pp 584-592.

2-Adins, A., Applications de la Pompe a Anneau Liquide dans l’ Industrie Quimique Vide Couches Minces, N 228 Ag.- Oct., 1985.

3-Asquith, W, Venting of Surface Condensers, Siemens Zeit, V 34 N3 Mar 1960.pp 150-155.

4-ASME, Performance Test Codes: Compressors, Vacuum Pumps and Blowers, PTC 9-1970

5-Bacaranda, P, Vacío, Conceptos Básicos, Universidad de los Andes, 1981.

6-Badger, W. L, Heat Transfer and Evaporation, Chemical Catalog Co, New York, 1956. p 224.

7-Baumeister, et al, Standard Handbook of Mechanical Engineers, Eigth. Edit., Mc Graw Hill, 1984

8-Brooks, E., Choosing The Right Vacuum Pump, Mach. Des. V 49 N1 Jan 6 1977 pp83-87

9-Cancio, E.Técnica de Vacío, MIBSA, Madrid, 1988

10-Carrillo Mora, P., Cálculo de la Capacidad de las bombas de Anillo Líquido, Trabajo de Diploma, 1991, Tutor Ing. Osvaldo García Morales.

11-Castro Ruz, F. Discurso Pronunciado en el Acto Central por el XXX Aniversario de los C.D.R., La Habana, 28 set. 1990, Granma 1 de Octubre de 1990.

12-          Discurso Pronunciado en el I Forum Nacional de Energía, 4 Dic. de 1984, Edit. Política, La Habana, 1984

13-           Discurso Pronunciado en la Clausura del IV Congreso de la Federación Estudiantil Universitaria, La Habana, 20 Dic. 1990, Granma 31 Diciembre de 1990

14-Caudala, J. P., Le Pompage de Vapeurs au Moyen de Condenseurs, Vide Couches Minces N 228 Ag.- Oct., 1985, pp 137-148.

15-C.Z.N. 107060-1984, Máquinas Neumáticas Mecánicas, Métodos de Medición de los Parámetros.

16-Cambers, A. Vacuum Pumps and Systems, Plant Eng. (Barrington III) V 31 N12, Jun 9, 1977 pp 141-145.

17-          Vacuum Pumps and Systems, Plant. Eng. (Barrington III), V 31 N17.Aug.19, 1977 pp 129-133.

18-Cherkassky, V.M, Bombas, Ventiladores, Compresores, Edit. MIR, Moscú, 1986.

19-Chilvers, R.H. and D.G. Love, Measuring Vacuum Pump Performance, The Southafrican Sugar Journal, Dec. 1986, pp 417-420.

20-Chlumsky, V., Reciprocating and Rotary Compressors, Published of Technical Literature, Prague, 1965, 515 p

21-Cummins, L., Liquid Ring Vacuum Pump Optimize Power Generation, World Pumps, Jan 1987, pp14-15.

22-Dobrobolsky, Elementos de Máquinas, Edit. MIR, Moscú 1980

23-Diels, R. and Jaccket, R. Leybold Vacuum Handbook, Pergammon Press, 1966.

24-Florescu, N.A, On Measurement of Speed of Vacuum Pump, Applied Sci. Research Sec. B V 7 N 1, 1958, pp 63- 62.

25-García Morales, O. y Néstor Ramos Páez, Cálculo de la Capacidad de las Bombas de Vacío de Anillo Líquido, Ingeniería Energética, V XV N 2, 1994.

26-García Morales, O. y Néstor Ramos Páez, Influencia Energética de las Infiltraciones en los Tachos de la Industria Azucarera, Ingeniería Energética, V XVI N 2, 1995.

27-García Morales, O, N. Ramos y M. Valera, Cálculo de Diseño de las Bombas de Vacío de Anillo Líquido, Ingeniería Energética, V XVI N 2, 1995.

28-García Morales O. y Otros, Estudio del Estado Constructivo de las Bombas de Vacío 3000 y 1500 Producidas en la EMPROMEC “Primero de Mayo”, Informe Técnico, Matanzas, 1995.

29-García Morales O. y N. Ramos, Estudio de los sistemas de vacío de los centrales azucareros, III Congreso Iberoamericano de Ingeniería Mecánica, La Habana, 1997.

30-García Morales O. y N. Ramos, Influencia de la Temperatura del Agua de Enfriamiento en el Consumo Específico de Energía de las Bombas de. Anillo Líquido, Segunda Reunión de Fluidodinámica y sus Aplicaciones Cuba’96, Universidad de Matanzas, Enero de 1996.

31-García Morales O. y Néstor Ramos Páez, Ahorro de Energía en Bombas de Vacío, Conferencia Internacional de Ahorro de Energía, CIAE ‘95, Universidad de Matanzas, Mayo de 1995.

32-García Morales O., N. Ramos y S. M.Suárez, Ahorro de Energía en Sistemas de Vacío, 44 Conferencia Nacional de la ATAC, Central Humberto Alvarez, Matanzas, 1995

33-Green, C.F., Liquid Ring Vacuum Pumps, Brit. Chem. Eng. , V 16 N 1, Jan 1971.

34-Gregorov, V.P, et al, Effect of the Pressence of a Liquid in the Outlet Gas on the Performance of a Liquid Ring Vacuum Pump, Chem. Pet. Eng.V 22 N 4, Mar.- Apr. ,1986, p 129.

35-Gibbs. C.W, To Create Vacuum, Compressed Air Magazine, V 72 N 6, June, 1967, pp 10- 16.

36-Gómez, J., Calculate Air Leakage Values for Vacuum Systems, Chem. Eng. , V 98 N 6, .1991.

37-GOST 25662- 83, Equipos de Vacío, Bombas de Vacío, Parámetros. Requisitos. Métodos de Ensayo.

38-Guthrie, A., Vacuum Technology, New York, 1965.

39-Gutiria, S., Rodamientos, Departamento de Ingeniería Mecánica, ISAI Camilo Cienfuegos, Matanzas, 1988.

40-Hansen, Joseph P., Rotary Vacuum Pumps Remove Condenser Air. , Eng. Rev., V 40 N 1, 1975 pp 4-7

41-Hanning J., Utilization de Cascades de Roots en Pompage Chimique, Vide Couches Minces N 228,  Aug- Oct 1985 pp 101-105.

42-Huff, George, Selecting a Vacuum Producer, Chem. Eng. , V 83 N 6,Mar 15 1976, pp 83-86.

43-Hugot, E., Handbook of Cane Sugar Engineering, Second Edit., Elsevier Scientific Publishing Co. , Amsterdam, 1972.

44-Huse, H., Liquid Ring Vacuum Pumps Aid Boiling Control, Sugar y Azúcar, Dec 1965 V60 N 12.

45-Hull, L.w., Pick a Vacuum System for your Job, Chem. Eng. , V 60 N11, Nov 1953.

46-ISO 1607-1980. Positive Displacement Vacuum pumps. Measurement Characteristics.

47-Izvestiya Vysshikh Uchebnykh Zabebedenii, Ideal Work Cicle and Theoretical Indicator Diagrams of two Rotors Vacuum Pump with Partial Internal Compression, Machinostroeienie, N 10 1964, pp 119- 132.

48-JIZ B 8316- 1985, Bombas Giratorias de Vacío Selladas con Aceite. Medición de Características de Funcionamiento.

49-Maa, J. R., Gas Flow Trough Anular Gap. Science and Technology, V 5 N 5 Sep-Oct 1968.

50- Justis, E. J and Eberhart, Evaluation of Vacuum Pump Drive Capital Costs, Tappi V42 N8 Aug 1959 pp 678-83

51- Karassik, et al, Manual de Bombas, Mc Graw Hill, New York, 1976.

52- Kirk and Othmer, Encyclopedia of Chemical Tecnology, Vol.14 Interscience Publishers, Ininc, New York, 1955.p 514.

53- Kocwin, M.J, Flussigkeitsring Pumpen Zum Forderm Von Gasen Und Dampfen, Technishe rumdschau Zulzer, 1973 No. 2, V 63.

54- Kovats, A Design and Performance of Centrifugal and Axial Flow Pumps and Compressor, Pergammon Press, Oxford, 1964, 468 p.

55- Kusay, R.G.P, Vacuum Equipment for Chemical Processes, Brit. Chem. Eng. V 16, N 1, 1971.

56- Lopez Marrero, O. Estudio Sobre Pruebas de Hermeticidad, Trabajo de Diploma, Universidad de Matanzas, 1992, Tutor Ing. Osvaldo García Morales.

57- Lorenzi Antonio, Two Fase Flow Rate Measurement with Sharp-edge Orifices. Theoritical Analysis, Termotécnia (Milán), V 31 N 3, Mar 1977 pp 119-27.

58- Luwig, E, Applied Process Design for Chemical and Petrochemical Plants, Huston Texas, Gulf, 1965.

59- Lubenets, V.D, Calculation of Internal Leakage in Rotary Vacuum Pumps. Machinostroenie, N 5, 1965, pp 84-86.

60-Lubenets, V. D.,Estimation of Effect of Varius Factors on Performance of Low Vacuum Systems, Machinostroeienie N 11 1965 pp 80- 85.

61-Lubenets, V. D., Method of Determining Distribution of Losses in Vacuum Pumps, Machinostroenie N 4 1965 pp 90-98.

62- Mathy C., Pompes  et Compressiurs a Anneau Liquide Optimization Des Utilities, Vide Couches Minces N 228 Ag.-Oct 85 Supp 161-170.

63- Maurice, L. , La Maitrice de L’ Energie Dans Le Installations, Vide Couches Minces N 228 Ag.-Oct 1985 Suppl 281-293.

64- Mendiola Suárez, J.A, Pruebas de Hermeticidad, Trabajo de Diploma, universidad de Matanzas, 1993, Tutor. Ing, Osvaldo García Morales.

65- Mengorix, J., Experimental Study of Ouput Rate of Sonic Flow  from Sharp Edged Orifices, Acad Des Sciences   Cr V 267 Ser A N 11 Sep 9, 1968 pp 400-402.

66-MINAZ, Indice de Capacidades de Ingenios de Crudos de Cuba, Edit Ciencia y Técnica, La Habana, 1972

67- Moffat, R, Putting Industrial Vacuum To Work, Hydraul Pneum, V 40 N 5 May 1987 p 58-63.

68- Monroe, E.S, Vacuum Pumps Can Conserve Energy, Oil Gas J. V 73  N 5 Feb.3, 1975 pp 126-128.

69-NASH Engineering Co. , Nash CL Vacuum Pumps, Bulletin N 472 G, Norwalk, Conn. , 1971.

70-NASH International Company, The Application of Nash Liquid Ring Pumps and Compressors in the Sugar Industry, Bulletin N427 B, Norwalk, Conn., 1974.

71-Nichols, B., Vacuum Pumping Systems Pumps Pumpes Pumpen N 100, Jan. 1975 pp 570-73.

72-Noel, P., Methodes de Detectides des Fuites en Tecnique du Vide. Rev. Francaise de Mecanique N 21, 1967 pp 5-13.

73-NRA 085: 1986 Industria Azucarera. Evaporadores de Guarapo. Prueba y Ajuste. Aprobada 1986- 03 Vigente 1986- 05

74-Oatley, C.W., Experimental Determination of Speed of Vacuum Pump and of Components of Vacuum Systems, Applied Phisics V 5 N 10 Oct. 1954 pp358-62.

75-Paugham, L., Economies de Energie sur les Installations Industrielles Funnctionant sous Vide avec Pompe a Vide a Anneau Liquide, Vide Couches Minces N228 Ag.- Oct 85

76-Pavielko, V., Sistemas de Utilización del Calor en las Industrias, Parte III, Departamento de Termoenergética, ISAI Camilo Cienfuegos, Matanzas, 1989.

77-Pedroni, J. M., Diseño de Sistemas de Vacío, Ing. Quim. (Madrid) V20 N228, 1988  pp119-123

78-Pérez Sotolongo, N., Determinación de Incondensables, Trabajo de Diploma, Matanzas 1995, Tutor Ing. Osvaldo García Morales.

79-Perry, R.H and Chitton C.H., Chemical Engineers´Handbook, Ed. Rev., La Habana, 1986.

80-Pfleiderer, C., Bombas Centrífugas y Turbocompresores, Edit. Labor, S.A, Barcelona, 1960.

81-Perk, C.G, Process 9th Congress, ISSCT, 1956, p 89.

82-Pipko A., et al, Fundamental of Vacuum Techniques, Edit. Mir, Moscú 1985.

83-Popov B. D., et al, Protzessi y Apparati Pijsheby Proisbodst, Edit. Vishaya Shkola, Moscú, 1976.

84-Poey J. I. , Cálculo de la Capacidad de las Bombas de Anillo Líquido, Trabajo de Diploma 1991. Tutor Ing. Osvaldo García Morales.

85-Roth A., Calculation of Leaky Vacuum Installation Brit. Chem. Eng. V 6 N1 Jan 1961 p 40- 44.

86-Ryerson, D. E. ¿ How Big is your Effet Vacuum Pump?, Procedings of the Quensland Society of Sugar Cane Technologists, 38 Conf. , Cairns, Quensland, April 1971.

87-Rynas, J. L., Application of Basic Energy Conservation Principles to the Disign of Rough Vacuum Systems, ASME Paper 76- WA/ PID- 17 for meet Dic 5, 1976, 12 p.

88-Solem, P., Siemens Water - sealed Vacuum Pumps as Compact Units for the Deareation of Steam Turbine Condensers, Kraftswerkstech V 56 N 11 Nov 1976 pp677- 682.

89-Sobieszek, T., Evaluación Ecológica de Gases y Vapores, Revista Técnica Sulzer, 3 / 4, 1986.

90-Spinks, W., Vacuum Technology, Chapman and Hall, 1963.

91-Von Waerabeke, P., L´ Eyecteurs et le Prix de l´ Energie, Vide Couches Minces N 228 Ag.- Oct. 1985

92-                               Vide et Economies d´ energie, Vide Couches Minces N 228 Aug- Oct. 1985 Suppl. P 183-194.

93-Varios, Manual de Operaciones para Producción de Azúcar Crudo de Caña, Dirección de tecnología del Ministerio del Azúcar, la Habana, 1995.

94-Van Atta, Vacuum Science and Engineering, Mc Graw Hill, New York, 1965.

95-Venema, A., La Mesure du Debit d´um Pompe a Vide. Le Vide V14 N81 May- Jun 1959 pp 113- 20.

96-Wallas, S., Rules of Thomb. Selecting and Designing Equipment, Chem. Eng. March 16, 1987 p 75, V94 N 4.

97-Yeates, C. S.. , Some Practical Aspects of Leak Detection And Leakage Evaluation in Vacuum Plants. The Quality Engineer V 34 N 2, 1970.

 

 

                                                                                                                 ANEXO.

Tabla 4.2.Parámetros reales, de cálculo y variación en bombas cubanas.

 

 

 

 

Modelo 4003

Modelo 2003

Modelo 1003

 

Parámetro

 

real

 

calculado

% variación

 

real

 

calculado

% variación

 

real

 

calculado

% variación.

Espesor álabes s (mm)

20

21

5

20

20

0

10

10

0.

Radio exterior ra (mm)

453

457

0,8

316,5

310

1,9

229,5

223

2,8.

Longitud axial b (mm)

392

377

3,8

275

273

0,7

184,5

190

2,9.

Radio interior ri (mm)

187

189

1,07

117,5

115

2,1

96

93

3,1.

Angulo j  (grados)

289

290,9

0,3

290

290,2

0,07

290

291,1

0,01.